Tóm tắt
Thí nghiệm cơ học theo các đường chất tải khác nhau (gia tải đều theo các phương và theo tỷ lệ gia tải khác nhau giữa áp lực ngang và áp lực đứng) đã được tiến hành trên cát kết có độ cố kết yếu Otter Sherwood, được lấy từ vết lộ đá tương đương đá vỉa của mỏ dầu Wytch Farm (Vương quốc Anh). Ứng xử cơ học đàn hồi và biến dạng dẻo đã xuất hiện và được dùng để xác định ứng suất giới hạn, đồng thời hoàn toàn phù hợp với mô hình Cam-clay hiệu chỉnh vàmô hình mũ elipse cho tất cả ứng suất giới hạn dẻo.
Từ khóa: Cơ học, vỉa cố kết yếu, đường chất tải, mỏ dầu Wytch Farm, cát kết Sherwood.
1. Giới thiệu
Trong quá trình khai thác dầu khí, áp suất vỉa suy giảm (depletion) làm gia tăng ứng suất hiệu dụng trong khung đá. Sự thay đổi này phụ thuộc vào tính chất của đá, đồng thời cũng là tác nhân làm vỉa bị nén lại. Trong trường hợp bất lợi, phần biến dạng dư và sự giảm lỗ rỗng không phục hồi có thể gây ra hiện tượng sụt lún trong khu vực khai thác dầu khí, dẫn đến các hậu quả nghiêm trọng như: ống dẫn bị vỡ, độ thấm giảm, phải dừng khai thác [1]. Độ rỗng của vỉa cát kết có độ cố kết kém thường lớn và giảm nhiều nếu chịu sự gia tải của ngoại lực. Do đó, dự báo biến dạng của đá, hiểu được bản chất của cơ chế nén của vỉa sẽ giúp kiểm soát và tối ưu hóa việc khai thác vỉa sản phẩm.
Theo các nghiên cứu trước đây về hiện tượng sụt áp suất gây ra sự nén vỉa, các thí nghiệm mô phỏng đường chất tải bằng thí nghiệm biến dạng một trục (trường hợp oedometric: chỉ có biến dạng thẳng đứng, không có biến dạng ngang) [3] hoặc thí nghiệm nén đều theo các phương [2], dễ thực hiện trong phòng thí nghiệm.
Tuy nhiên, tại khu vực khai thác dầu khí hiếm khi tìm thấy trạng thái ứng suất đẳng hướng; mà thường ứng suất thẳng đứng và ứng suất ngang tăng đồng thời trong quá trình khai thác. Segura [4] giả thiết rằng còn có ảnh hưởng của hiệu ứng ứng suất vòm gây ra sự phân bố lại của ứng suất thẳng đứng trong quá trình vỉa bị nén. Đối với trường hợp biến dạng một chiều, điều kiện biên cần được thỏa mãn là tỷ lệ kích thước của vỉa phải rất lớn (nghĩa là chiều dày theo phương thẳng đứng rất nhỏ so với chiều ngang của vỉa). Ruistuen [5] đã chứng minh điều kiện biên này trong bể chứa là không chính xác và điều kiện biến dạng một phương không đúng trong nhiều trường hợp. Những điều kiện biên này phụ thuộc vào nhiều thông số: kích thước và hình dạng của vỉa chứa, sự tương quan giữa tính chất rỗng, đàn hồi giữa vỉa và đá xung quanh, tính biến dạng không phục hồi của chúng.
Để mô phỏng phù hợp với sự thay đổi ứng suất tại hiện trường trong quá trình khai thác, Rhett và Teufel [6] đã xác định thông số đường chất tải bằng tỷ số thay đổi ứng suất hiệu dụng ngang và thẳng đứng, so với ứng suất ban đầu. Theo định nghĩa này, trường hợp nén đẳng hướng tương đương với K = 1, trong khi đó thí nghiệm nén 3 trục cổ điển tương ứng với hệ số K = 0. Rhett và Teufel [6] đã chỉ ra rằng các giếng khai thác dầu tại Ekofisk có giá trị đường chất tải K = 0,2. Tuy nhiên, từ những thí nghiệm mô tả trong phòng thí nghiệm trong trường hợp biến dạng 1 trục lại chỉ có hệ số K nằm trong khoảng 0,4 - 0,6, tùy thuộc vào từng loại đá. Do vậy, đường chất tải K cần phải lựa chọn theo tính chất của từng loại đá, và cần phải được so sánh bằng phép đo thực tế tại hiện trường. Thông thường, các kỹ sư dầu khí thường dung mối quan hệ thông số đường chất tải với hệ số Poisson hay thông số đặc trưng cho tính chất đàn hồi của đá K =v/(1-v), hệ số trong trường hợp này thường được ký hiệu là Ko đồng thời cũng nhận được từ thí nghiệm nén 1 trục [5, 7].
Nhiều nghiên cứu đã chỉ ra rằng ứng xử nén của đá vụn silic và đá carbonate hoàn toàn giống nhau ở mức độ macro trong điều kiện nhiệt độ thấp [8, 9] nhưng cơ chế lại khác nhau hoàn toàn ở mức độ micro. Tính nén không hồi phục thường liên quan tới hiện tượng vỡ các hạt đá và cấu trúc lỗ rỗng bị vỡ. Áp suất gây vỡ các hạt đá có thể được dự đoán bằng quy luật của Zhang [10] đối với các loại đá vụn silic. Quy luật này được xây dựng dựa trên mô hình phá hủy Hertz hoặc mô hình vỡ cấu trúc lỗ rỗng dùng cho loại đá carbonate [11]. Khi áp suất tác dụng đạt tới giá trị giới hạn này, biến dạng giòn hoặc dẻo sẽ xuất hiện và tương ứng là dạng phá hủy giòn hoặc hiện tượng phá vỡ cấu trúc lỗ rỗng, gây ra hiện tượng suy giảm tính thấm nhanh chóng.
Theo quan điểm của tính thủy cơ học, nhiều tác giả [5, 6, 12, 13, 14] đã nghiên cứu ảnh hưởng của đường chất tải lên tính nén và tính thấm dọc (kv) (song song với phương ứng suất chính lớn nhất) cho nhiều loại cát kết hoặc là lấy từ tự nhiên hoặc là trực tiếp từ các vỉa chứa dầu khí.
Thông thường, các tác giả cho rằng tính thấm giảm theo đường chất tải, và càng giảm mạnh đối với đường chất tải có thông số K nhỏ. Ngược lại, có rất ít nghiên cứu phương pháp đo tính thấm ngang k¬h (theo phương vuông góc với ứng suất lớn nhất). Zhu [15] đã đo tính không đồng đều của độ thấm bằng cách dùng phương pháp dòng chảy thẳng đứng đối với máy nén 3 trục khi thí nghiệm dạng “kéo”. Một phương pháp khác do Crawford [16] và Dautriat [17] đề xuất là đo tính không đồng nhất độ thấm bằng cách cho dòng chảy nhanh qua mẫu nghiên cứu (phương pháp không truyền thống), sau đó hiệu chỉnh công thức tính độ thấm của Darcy bằng hệ số hình học có xét tới hình dạng chảy phức tạp trong mẫu [18].
Một vấn đề khác cũng cần đề cập khi đo độ thấm đó là hiệu ứng tại mép mẫu nghiên cứu lên tính cơ thủy lực sau mỗi lần tăng lưu lượng dòng chảy qua mẫu [17, 19, 20].
Từ những số liệu về độ thấm đã đo từ phòng thí nghiệm và hiện trường, có thể tính toán được chỉ số khai thác PI đặc trưng cho khả năng khai thác dầu khí của vỉa chứa [21, 22].
Để mô hình ứng xử thủy cơ học nhận được từ phòng thí nghiệm theo các đường chất tải khác nhau K, Crawford [23] đã sử dụng mô hình Cam-clay hiệu chỉnh (elipse đối xứng) thuộc loại mô hình đàn hồi - dẻo để mô hình hóa các dữ liệu của loại cát không cố kết dưới tác dụng của các đường chất tải khác nhau, sau đó dự đoán sự thay đổi của độ thấm theo biến dạng [24]. Các tác giả đề xuất sử dụng hệ số hiệu chỉnh tâm đối xứng elipse không trùng với gốc tọa độ của hệ trục. Các thông số đàn hồi - dẻo như module Young E, hệ số Poisson v , hệ số tăng bền λ và hàm thế dẻo có thể nhận được bằng cách đồng nhất đường dữ liệu thí nghiệm và mô hình lý thuyết như đã được mô tả trong các tài liệu [25 - 28].
Trong bài báo này, nhóm tác giả giới thiệu ứng xử cơ học của cát kết có độ cố kết yếu, thuộc độ tuổi Triassic; tương ứng với loại cát kết Sherwood hay chính là đá vỉa tại mỏ dầu Wytch Farm thuộc tỉnh Dorset, Vương quốc Anh, được BP khai thác từ những năm 80 của thế kỷ XX và gần đây đã bán lại cho Perenco. Sau khi nghiên cứu lựa chọn vật liệu và thiết bị thí nghiệm cơ học cho các loại đá khác nhau, phục vụ đo độ thấm theo các phương khác nhau, nhóm tác giả giới thiệu các kết quả thí nghiệm. Bài báo phân tích các vấn đề cơ bản về ứng xử cơ học của các loại đá khác nhau và việc sử dụng mô hình đàn hồi - dẻo để dự báo độ biến dạng cho một đường chất tải bất kỳ.
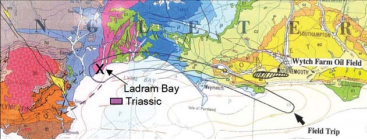 |
| Hình 1. Sơ đồ miền Nam nước Anh với vùng
đá độ tuổi Triassic lộ thiên [hiệu chỉnh từ 34]; vị trí vịnh Ladram
(tỉnh Devon) và nơi mẫu cát kết được mang về phòng được đánh dấu; vùng
khai thác dầu khí Wyth Farm |
 |
 |
| Hình 2. Vết lộ trầm tích ở vịnh Ladram, nơi lấy mẫu cát kết Sherwood |
Nghiên cứu và kết quả được giới thiệu trong bài báo là nội dung cơ sở trong việc xây dựng mô hình địa cơ học phục vụ công tác khoan như tối ưu năng suất khoan, ổn định thành giếng khi khoan và trong quá trình khai thác dầu khí như hiện tượng sinh cát, nứt vỉa thủy lực được áp dụng tại vỉa dầu Wytch Farm. Nhóm tác giả dự kiến phát triển đề tài trong việc tổng hợp các ứng dụng của mô hình địa cơ học trong công nghiệp dầu khí, thực hiện thí nghiệm, xây dựng mô hình địa cơ học trên vỉa cát kết Miocene trung thuộc bể trầm tích Cửu Long, vỉa cát kết Miocene hạ thuộc bể Nam Cơn Sơn.
2. Mô tả cát kết
 |
 |
 |
| Hình 3. Lát cắt thẳng đứng mẫu cát kết
Otter Sherwood: Hình ảnh phóng to một vùng có chiều rộng 1mm (a); Quan
sát bằng kỹ thuật quét dưới kính hiển vi điện tử (SEM) chỉ rõ khoáng
chiếm đa số trong mẫu là: Quartz (b) và Feldspar(c) |
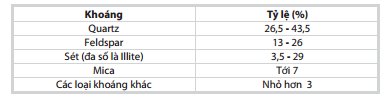 |
| Bảng 1. Thành phần khoáng trong cát kết Otter Sherwood [29] |
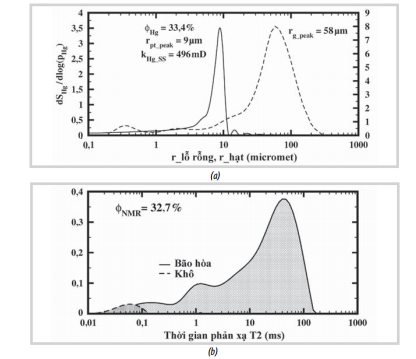 |
| Hình 4. Phân bố bán kính hạt trong mẫu
OSS bằng đo nhiễu xạ ánh sáng, đa số các hạt có bán kính 58µ m, phân bố
bán kính lỗ rỗng, đa số có bán kính 9 µ m và nhỏ nhất là 0,01 µ m (a);
phân bố thời gian hồi phục T2 bằng kỹ thuật NMR cho mẫu OSS khô và mẫu
bão hòa (b). |
Cát kết có độ liên kết kém Otter Sherwood (ký hiệu là OSS) được xếp vào loại đá feldspar [29]. Loại cát kết này thuộc tuổi Triassic [30, 31] và là một loại đá vỉa trong mỏ dầu Wytch Farm. Vỉa OSS nằm ở độ sâu trung bình 1.585m so với mực nước biển [32, 33]. Mẫu nghiên cứu được lấy từ vịnh Ladram gần tỉnh Devon (Hình 1 và 2). Các mẫu được khoan tại chỗ theo phương vuông góc (V) và song song (H) với phương trầm tích thẳng đứng (Hình 2).
Lát cắt mỏng được chuẩn bị để quan sát cấu trúc của đá (Hình 3): màu xanh của keo dính chiếm phần lớn trong mẫu thể hiện độ rỗng cao, còn lại các dải băng đen nằm xen kẽ và chia các vùng khoáng Quartz màu trắng.
Thành phần khoáng trong OSS (Bảng 1) đã được Svendsen và Hartley [29] nghiên cứu. Lát cát mỏng được phân tích trong Hình 3a phù hợp với kết quả đó.
Kích thước hạt của mẫu được nghiên cứu bằng kỹ thuật đo nhiễu xạ ánh sáng (Hình 4a). Kích thước hạt xuất hiện trong mẫu nằm từ 10 - 500 µ m. Quan sát thành phần hạt bằng kỹ thuật quét dưới kính hiển vi điện tử (SEM) (Hình 3) cho thấy các khoáng chính trong mẫu là Quartz và K-Feldspar với kích thước hoàn toàn phù hợp với kỹ thuật đo nhiễu xạ ánh sáng.
Trong Hình 4a, đường cong liền là kết quả của kỹ thuật bơm thủy ngân vào mẫu cho thấy sự phân bố kích thước lỗ rỗng trong mẫu, với đa số bán kính lỗ rỗng khoảng 9mm. Độ rỗng của OSS đo được bằng phương pháp bơm thủy ngân là 33,4%, và 32,7% bằng kỹ thuật NMR (Hình 4b). Độ thấm tính toán bằng phương pháp bơm thủy ngân Hg (công thức Swanson) là 496mD.
3. Thí nghiệm
3.1. Máy nén thủy lực 3 trục và các đo đạc
Máy nén thủy lực 3 trục dùng cho nghiên cứu này (Hình 5) hoạt động thông qua 2 bơm áp suất lên tới 69MPa và có thể hoạt động độc lập để điều khiển sự thay đổi áp lực nén ngang và nén dọc. Các đường chất tải khác nhau được thực hiện bằng cách thay đổi vận tốc gia tải của bơm áp suất. Áp lực lỗ rỗng được khống chế bằng bộ điều khiển tự động. Dòng chảy qua mẫu được thực hiện bằng bơm thứ 3 có áp suất tối đa thấp hơn (25MPa) [17].
Để đo được chuyển vị dọc và ngang lớn cho trường hợp mẫu có độ cố kết thấp (tới vài mm), máy nén được trang bị thiết bị đo biến dạng thẳng đứng LVDT cho chuyển vị thẳng đứng và 1 cặp đo biến dạng ngang “Cantilerver”, luôn được ấn định trên mẫu. Biến dạng thể tích (εv) và biến dạng lệch (εQ) được tính từ biến dạng thẳng đứng (εa) và biến dạng ngang (εr) bằng công thức tương ứng như sau εv= εa + 2εr và εQ= 2(εa - εr)/3 với giả thiết rằng hình dạng mẫu trong quá trình nén luôn là hình trụ.
Độ thấm có thể được đo theo 3 phương vuông góc trên mẫu nghiên cứu. Theo phương thẳng đứng (phương ứng suất lớn nhất), độ thấm dọc kv được đo đồng thời tại 2 vị trí, trên toàn bộ chiều dài của mẫu (80mm) và trên khoảng cách trung gian của mẫu (60mm) tương ứng với vị trí của 2 điểm đo cố định trên membrane. Độ thấm ngang kh được đo từ 2 phương vuông góc nhau tại vị trí trên và dưới của mẫu. Sự xác định hệ số hình học G, đã được kiến nghị để hiệu chỉnh công thức của Darcy trong kỹ thuật đo độ thấm ngang [16 - 19]. Để theo dõi áp suất lỗ rỗng, áp lực chất lỏng bơm vào và ra mẫu cũng được ghi lại trong suốt quá trình thí nghiệm.
Nghiên cứu độ thấm và mối liên hệ với tính chất cơ học của vỉa là công việc tiếp theo của dự án này trong tổng thể công việc xây dựng mô hình địa cơ học áp dụng cho công tác khoan, khai thác và mô hình vỉa dầu.
3.2. Quá trình thí nghiệm nén
Tham số đường chất tải K [6], được định nghĩa tương ứng với hệ số η, là góc nghiêng của đường thẳng tuyến tính trong hệ trục tọa độ (P’, Q) thông qua quan hệ η = 3(1 - K)/(1 + 2K) (Hình 6); P ' = (δa + 2Pc' ) / 3 là ứng suất trung bình hiệu dụng và Q= δa + Pc' là ứng suất lệnh. Do vậy, việc dùng tham số đường chất tải K để mô tả đầy đủ tính thủy cơ học của OSS: (1) Nén đẳng hướng thoát nước K = 1; (2) Nén 3 trục theo đường chất tải tỷ lệ K = 0,8; 0,6; 0,4; 0,2 và (3) Đường nén 3 trục cổ điển K = 0 (áp suất nén ngang không đổi), tức là chỉ tăng gia tải theo phương thẳng đứng với tỷ lệ ứng suất σa = 0,1MPa/ phút được lựa chọn để tương ứng với biến dạng єa trong khoảng 1 x 10-5 đến 4 x 10-7s-1. Vì OSS có tính thấm cao nên điều kiện thoát nước luôn luôn được đảm bảo.
4. Chuẩn bị mẫu
Mẫu thẳng đứng (V) và ngang (H) đã được khoan tương ứng theo phương vuông góc và song song với các lớp trầm tích, chiều dài mẫu là 80mm và đường kính là 38mm. Các mẫu được làm khô trong tủ sấy ở nhiệt độ 60oC, trong thời gian tối thiểu 48 giờ. Tiếp theo, phân bố khối lượng riêng dọc theo mẫu được nghiên cứu bằng phương pháp X-quang. Mẫu có phân bố đồng đều tiếp tục được chọn để nghiên cứu thí nghiệm cơ học.
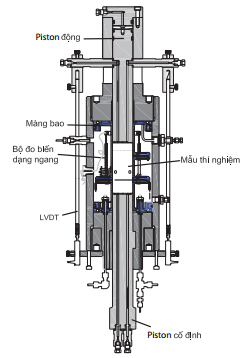 |
| Hình 5. Máy nén thủy lực 3 trục |
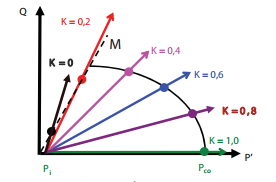 |
| Hình 6. Các đường chất tải sử dụng để
nghiên cứu phản ứng tính thủy cơ học của cát kết Otter Sherwood: K = 0,
ứng với thí nghiệm nén 3 trục cổ điển, và K > 0, ứng với đường chất
tải tỷ lệ |
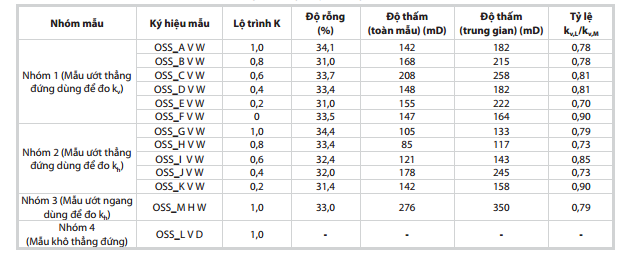 |
| Bảng 2. Các thông số cơ lý của mẫu nghiên cứu |
Ban đầu mẫu ở trạng thái khô và được tăng tải đều theo các phương cho tới 2MPa để đảm bảo độ chặt giữa mẫu và màng chống thấm bao bọc quanh mẫu và đảm bảo cố định dụng cụ đo biến dạng ngang. Biến dạng ban đầu của mẫu được xác định để làm quy chiếu. Sau đó, mẫu được hút chân không trong thời gian tối thiểu 3 giờ và tiếp tục được bão hòa với áp suất bơm giữ không đổi 0,5MPa. Thể tích lỗ rỗng trong mẫu và độ rỗng được xác định bằng sự thay đổi thể tích của bơm (Bảng 2); vì trong mẫu OSS có chứa loại sét không nở, nên việc dùng dung dịch NaCl nồng độ 20g.L-1 là cần thiết để đảm bảo chắc chắn hơn không có sự ảnh hưởng trương nở của sét tới quá trình đo độ thấm. Sau đó, bơm 1 lưu lượng nước rất nhỏ chảy qua mẫu, với tổng thể tích bằng 3 lần thể tích lỗ rỗng trong mẫu, đảm bảo mẫu được bão hòa và không có bẫy khí trong mẫu cũng như trong hệ thống ống dẫn.
Cả 2 giá trị độ thấm dọc đều được đo ở trạng thái ban đầu bằng phương pháp dòng chảy ổn định với lưu lượng nằm trong khoảng 0,2 - 2cc/phút. Nhiệt độ phòng luôn được giữ ổn định ở 20oC để đảm bảo độ nhớt của chất lỏng và độ chênh áp giữa 2 điểm đo ổn định. Đối với nhóm mẫu ngang, việc đo độ thấm dọc cho giá trị độ thấm ngang tại hiện trường của trầm tích. Các thông số địa vật lý của mẫu được thống kê trong Bảng 2. Hình 7 cho thấy không có bất kỳ mối liên hệ trực tiếp nào giữa độ rỗng và độ thấm ở trong mẫu OSS.
 |
| Hình 7. Quan hệ độ thấm theo phương thẳng đứng và độ rỗng cho 11 mẫu, tương ứng số liệu trongBảng 2 của nhóm 1 và nhóm 2; độ rỗng trung bình là 32,75% và độ thấm trung bình là 181mD |
5. Số liệu cơ học
5.1. Gia tải đều
Số liệu cơ học dưới sự gia tải đều (K = 1) cho mẫu khô và mẫu bão hòa (Hình 8 và 9). Ứng suất nén gây ra biến dạng được quy ước là dương. Trong quá trình nén, biến dạng thể tích của mẫu qua 3 giai đoạn: (1) thể tích thay đổi nhanh khi áp suất tăng từ 2 - 5MPa tạo khả năng sắp xếp lại các hạt, đóng các vết nứt đã có từ trước và giảm độ rỗng; (2) đường tăng tuyến tính biểu thị biến dạng thể tích theo ứng suất trung bình hiệu dụng, đây chính là mô hình ứng xử tuyến tính của vật liệu; (3) quá trình nén diễn ra nhanh hơn biểu hiện bằng đoạn chuyển đổi độ cong trên đường ứng suất biến dạng. Trạng thái ứng suất tại vị trí điểm uốn tương ứng với sự thay đổi thể tích chuyển sang giai đoạn mới, hay tương ứng với việc chuyển từ ứng xử đàn hồi sang ứng xử dẻo của vật liệu. Sự xuất hiện của điểm biến dạng dẻo nhanh chóng (điểm ban đầu gây vỡ hạt) tương ứng với điểm giới hạn có kí hiệu là P*, được coi như chính là điểm kết thúc của biến dạng đàn hồi. Đối với cát kết Otter Sherwood giá trị ứng suất hiệu dụng trung bình này là P* = 39,5MPa và điểm uốn có giá trị xấp xỉ 50MPa. Các nghiên cứu trước kia đã chỉ ra rằng điểm xuất hiện của sự vỡ hạt tương ứng với điểm xuất hiện phá vỡ cấu trúc lỗ rỗng trong trường hợp gia tải đều và đã được kiểm nghiệm bằng ghi âm trong quá trình gia tải [10].
 |
| Hình 8. Thí nghiệm nén đẳng hướng trên
mẫu khô thẳng đứng, mẫu thẳng đứng và ngang bão hòa bằng nước muối NaCl
(a); Phân bố kích thước lỗ rỗng trên mẫu OSS_A V W (điểm cực đại tại bán
kính 7,6μm) được so sánh với mẫu nguyên dạng trong Hình 4a (b); Sự giảm
các lỗ rỗng sau khi nén (c) |
So sánh kết quả giữa các mẫu khô và mẫu bão hòa cho thấy mẫu không bị nén nhiều ở áp lực 2MPa; trong khi đó quá trình nén đàn hồi gần như tương đương giữa các mẫu, nhưng với mẫu khô thì áp suất tới hạn lớn hơn và lớn hơn giá trị 60MPa của máy bơm có thể đạt tới. Mẫu bão hòa được nén trong điều kiện thoát nước chỉ rõ độ bền nhỏ hơn độ bền của mẫu thí nghiệm khô (Hình 8a). Kết quả này cũng đã được kiểm nghiệm trên các loại đá cố kết từ các nghiên cứu trước (thông thường nhỏ hơn 25%) [35].
Độ cứng của các mẫu ngang là nhỏ hơn so với độ cứng của mẫu đứng trong vùng biến dạng đàn hồi và tương đối mềm hơn trong vùng biến dạng dẻo.
Độ rỗng giảm được xác định bằng biến dạng thể tích của mẫu khoảng 4,4p.u, và được kiểm tra là hợp lý đối với phương pháp đo thủy ngân có giá trị bằng 4,3p.u (Hình 8b); các lỗ rỗng có kích thước lớn hơn thì giảm nhẹ khoảng 1,5μm trong khi các lỗ rỗng có kích thước nhỏ (r < 0,1μm) thì hoàn toàn biến mất (Hình 8c); tỷ lệ lỗ rỗng nhỏ bị mất chiếm 50% trong tổng số lỗ rỗng bị giảm; độ thấm giảm được ước tính theo công thức của Swanson là 40%.
5.2. Gia tải theo đường chất tải
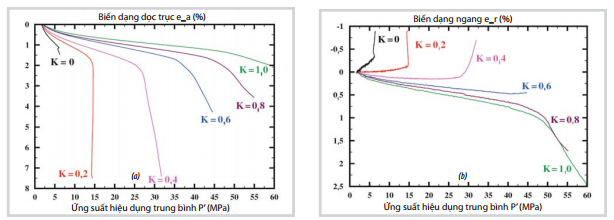
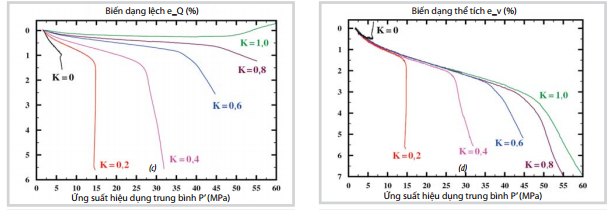
Đường chất tải được tiến hành thêm với K = 0,8; K = 0,6; K = 0,4; K = 0,2 và K = 0 được thực hiện trên 2 nhóm mẫu thẳng đứng (Bảng 2). Sự thay đổi biến dạng (dọc trục, ngang, lệch và thể tích) được thể hiện trong Hình 9.
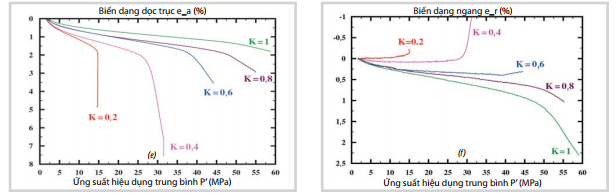
Giá trị K kiểm soát quá trình nén của mẫu đá dưới tác dụng của ứng suất hiệu dụng. Hình 9e và 9h cho thấy các đường chất tải đều có điểm chung ở giai đoạn 1 và 2 của biến dạng. Kết quả này tương tự với các kết quả nghiên cứu của Wong [8] hay Baud [10] đối với các loại cát kết cứng trong thí nghiệm nén 3 trục cổ điển. Các ứng suất hiệu dụng C* và C’ được định nghĩa bởi Wong [8] tương ứng với sự xuất hiện cơ chế phá hủy dẻo và giòn. Đối với gia tải lớn hơn giá trị giới hạn thì biến dạng thể tích gia tăng nhanh hơn so với kiểu gia tải đẳng hướng.
Xem xét chế độ biến dạng không đàn hồi cho thấy đa số các đường biến dạng dọc trục thể hiện tính biến dạng nén, các đường biến dạng ngang thể hiện dạng biến dạng nở đối với các đường chất tải có tham số K ≤ 0,6; thể tích của mẫu luôn nén lại trừ trường hợp thí nghiệm nén 3 trục cổ điển (K =0). Ngoài ra, biến dạng của mẫu tương đương trường hợp biến dạng một chiều đối với các đường gia tải nằm trong khoảng [0,2; 0,4]. Giới hạn ứng suất dẻo giảm đối với các đường chất tải có tham số K nhỏ.
 |
 |
 |
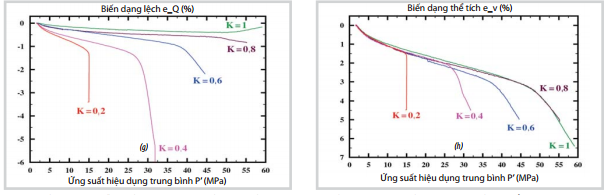 |
| Hình 9. Biến dạng của các mẫu cát kết OSS
theo các đường chất tải (a, e) biến dạng dọc trục, (b, f) biến dạng
ngang, (c, g) biến dạng lệch, (d, h) biến dạng thể tích/(bên trái) nhóm
1gồm các mẫu được khoan theo phương thẳng đứng và đo độ thấm dọc, (bên
phải) nhóm 2 gồm các mẫu khoan theo phương thẳng đứng và đo độ thấm
ngang |
 |
|
Hình 10. Chụp X-ray các mẫu OSS_F V W (K =
0), OSS_E_V_W (K = 0,2) và OSS_A_V_W (K = 0,1) trước và sau thí nghiệm
cơ học tương ứng (a, b), (c, d) và (e, f)
|
|
|
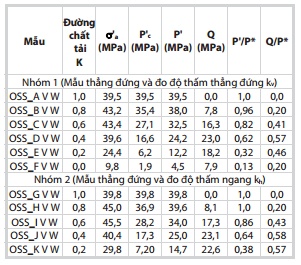
| Bảng 3. Các giá trị ứng suất giới hạn của
2 nhóm mẫu thí nghiệm;’a là ứng suất dọc trục hiệu dụng, P’c áp suất
nén ngang; P’ ứng suất trung bình hiệu dụng và Q là ứng suất lệch, được
chuẩn hóa bằng giá trị ứng suất hiệu dụng trung bình tiêu chuẩn P* =
39,5MPa đối với đường chất tải K = 1,0 |
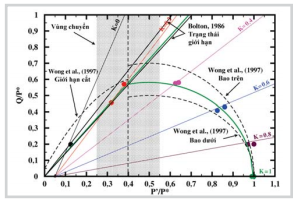 |
| Hình 11. Chuẩn hóa mặt chuẩn của cát kết OSS (với P* = 39,5 MPa), lựa chọn mô hình Cam-clay hiệu chỉnh và mô hình Wong được so sánh trên hình vẽ. Các giá
trị ứng suất giới hạn được vẽ bằng các điểm chấm trên hình và các đường
chất tải đi qua điểm giá trị ứng suất ban đầu đẳng hướng Po = 2 MPa |
Việc quan sát vùng chuyển ứng xử đàn hồi và dẻo càng thể hiện rõ đối với các trường hợp có tham số K nhỏ. Hai nhóm mẫu thí nghiệm có ứng xử cơ học tương đồng (trừ trường hợp K = 0,8) (Hình 9d và 9h). Do vậy, cát kết OSS có ứng xử cơ hóa học rất đồng nhất với quy mô kích thước mẫu thí nghiệm. Sau khi kết thúc thí nghiệm cơ học, mẫu được làm khô và tiến hành quan sát bằng X-ray với độ phân giải 1mm. Đối với trường hợp gia tải với hệ số K = 0 (Hình 10b), xuất hiện một vết nứt xiên chéo trong mẫu, thể hiện trạng thái phá hủy giòn của mẫu với các trường hợp gia tải có hệ số K nhỏ.
Vết nứt nằm ngang (Hình 10b) do quá trình lấy mẫu ra khỏi máy nén 3 trục, và cũng chính là vùng tập trung các khoáng vật mềm (sét, biotite). Đối với những đường gia tải K ≥ 0,4, độ phân giải 1mm không đủ để quan sát và xác định vùng biến dạng trong mẫu (Hình 10f ). Với đường chất tải K = 0,2 (Hình 10d) xuất hiện sự phát triển các dải băng cong ở phía 2 đầu mẫu, minh chứng chế độ biến dạng phức tạp trong mẫu thí nghiệm thuộc cơ chế phá hủy trung gian giữa phá hủy giòn và phá hủy dẻo.
5.3. Mô hình mặt giới hạn
Với kết quả thu được về cát kết có độ cố kết yếu thể hiện kiểu biến dạng đàn hồi - dẻo, vì thế một mô hình đàn hồi - dẻo kiểu mô hình Cam-clay hiệu chỉnh có thể mô tả được ứng xử của cát kết OSS. Các giá trị ứng suất giới hạn phân biệt giữa trạng thái biến dạng đàn hồi, dẻo được vẽ trong hệ trục tọa độ (P’, Q). Các điểm giới hạn trên đường cong biến dạng thể tích theo ứng suất hiệu dụng trung bình của 2 nhóm thí nghiệm. Quy ước truyền thống trong cơ học đá các điểm này là điểm cuối cùng của phần đoạn thẳng tuyến tính (sau điểm này biến dạng là không đàn hồi). Bảng 3 thống kê các điểm ứng suất giới hạn của các mẫu OSS tương ứng với các đường chất tải K.
Trong Hình 11, toàn bộ giá trị ứng suất giới hạn được chuẩn hóa và vẽ trong không gian ứng suất (P/P* x Q/P*).
Phương trình (1) đưa ra mặt giới hạn tương ứng với phương trình của mô hình Cam-clay hiệu chỉnh:
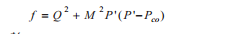 (1)
(1)
Trong đó:
M = (6sinφ/(3 - sinφ): Thông số của đường thẳng tiêu chuẩn Mohr-Coulomb;
φ: Ma sát kiểm soát kích thước hình dạng hình elipse;
Pco: Ứng suất tiền cố kết kiểm soát kích thước của elipse, và tương ứng với khả năng “lưu” giá trị áp suất trong lịch sử;
M tương ứng với góc nghiêng của đường giới hạn.
Thông số đường cong của mô hình Cam-clay hiệu chỉnh sát nhất với số liệu thí nghiệm là: M = 1,2 và P* = 39,5MPa.
Có 2 mặt chuẩn giới hạn được đề xuất bởi Wong và nnk [8]. Hai mặt giới hạn này được xác định từ thí nghiệm và tổ hợp bởi 6 loại cát kết với độ rỗng nằm từ 14,5 - 35%, và thí nghiệm bằng máy nén 3 trục. Ngoài ra, đường thẳngđi qua gốc tọa độ tương ứng là đường giới hạn mô tả giới hạn phá hủy giòn được xác định bởi Bolton [36], với số liệu của 17 loại cát khác nhau. Những giá trị ứng suất tương ứng ứng xử nén (hoặc cắt dạng nén) cũng có thể được fit bằng phương trình dạng elipse của Wong và nnk [8] mô tả bằng phương trình số (2):
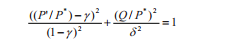 (2)
(2)
với các thông số P* = 39,5MPa; γ = 0,5; δ = 0,55.
Mô hình tĩnh này không đủ để mô hình hóa tính chất động của vật liệu, tức là vùng giới hạn biến dạng đàn hồi không phải là cố định. Ngoài ra, trong lịch sử gia tải và quá trình khai thác hydrocarbon, sự thay đổi gia tải lên các lớp địa tầng, vùng elipse có thể mở rộng ra (tương đương quá trình tăng vùng biên giới hạn biến dạng đàn hồi - gọi là quá trình tăng bền) hoặc vùng biến dạng đàn hồi có thể bị giảm - vật liệu bị mềm. Với mô hình Cam-clay hiệu chỉnh đi qua gốc tọa độ, có đỉnh của đường elipse trượt dọc trên đường thẳng giới hạn có thể mô hình hóa được kiểu ứng xử này của vật liệu.
Quan sát đường chất tải có hệ số K = 0,2, ứng xử của cát kết OSS hoàn toàn bị nén (Hình 9d và 9h); giá trị ứng suất giới hạn nằm ở vùng chuyển giao đặc trưng cho ứng xử trung gian của vật liệu giữa ứng xử giòn và dẻo, quan sát thấy các vằn cong chèn lên nhau (Hình 10d). Để phân tích chi tiết hơn về kiểu ứng xử này của vật liệu, cần bổ sung thêm một số thí nghiệm có đường chất tải nằm trong khoảng K = 0 và K = 0,4.
6. Mô hình cơ học
Kết quả thực nghiệm chỉ ra ứng xử cơ học của OSS là đàn hồi - dẻo do đó bước đầu nhóm tác giả đã tiến hành sử dụng mô hình được áp dụng phổ biến là Cam-clay hiệu chỉnh để phân tích kết quả cơ học đối với các đường chất tải và dự báo ứng xử thủy địa cơ học trong toàn bộ dự án.
Có 4 yếu tố đặc trưng cho mô hình này là: tính chất đàn hồi, đường giới hạn, hàm dẻo và quy luật chảy dẻo [25 - 28].
Đối với ứng xử vật liệu đàn hồi, các biến dạng coi như có thể phục hồi được như: biến dạng thể tích (є ve) và biến dạng cắt (lệch) (є qe), các biến dạng này đều có quan hệ với ứng suất hiệu dụng trung bình (P’) và ứng suất lệch (Q) theo phương trình sau:
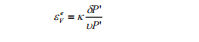 (3)
(3)
và (4)
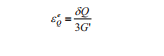 (4)
(4)
Trong đó:
κ: Hệ số nở;
υ: Thể tích đơn vị;
G’: Module cắt.
Đối với biến dạng dẻo, nếu giả thiết vật liệu là “chuẩn” thì hàm thế g sẽ trùng với hàm đặc trưng cho mặt giới hạn f trong phương trình (1): g = f. Khi đó vector mô tả sự gia tăng biến dạng có xu hướng vuông góc với mặt thế g, do đó:
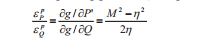 (5)
(5)
Với M là thông số tương tự trong phương trình (1), và η = Q/P’ là tỷ lệ ứng suất. Giá trị độ biến dạng thể tích được tính như sau:
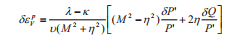 (6)
(6)
với λ là hệ số nén.
Các thông số của mô hình Cam-clay hiệu chỉnh và thông số đặc trưng đàn hồi được xác định trong Hình 12 và Bảng 4. Trong đó, eo là hệ số rỗng tại giá trị áp lực hiệu dụng trung bình P’ = 1MPa, hệ số thể tích biến cứng H được tính từ mối quan hệ: H = (1 + eo)/(λ - κ).
Đối với đá đồng nhất, ứng xử đàn hồi có thể được đặc trưng bởi 2 hệ số đàn hồi là module Young E và hệ số ν Poisson. Dữ liệu tương ứng với nhóm mẫu đã thí nghiệm cho hệ số E = 2,05GPa và ν = 0,31 và giá trị độ cứng thể tích K = 1,8GPa (Hình 8a).
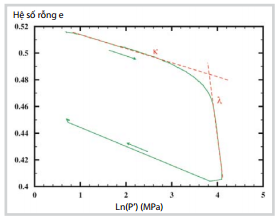 |
| Hình 12. Xác định các hằng số đàn hồi - dẻo κ và λ cho mẫu OSS A tương ứng với đường chất tải K = 1,0 và module đàn hồi K được xác định trên Hình 8a |
 |
Bảng 4. Bảng thống kê hệ số đàn hồi - dẻo đối với mẫu cát kết Otter Sherwood
|
Ghi chú: * giá trị ngoại suy từ các kết quả thí nghiệm
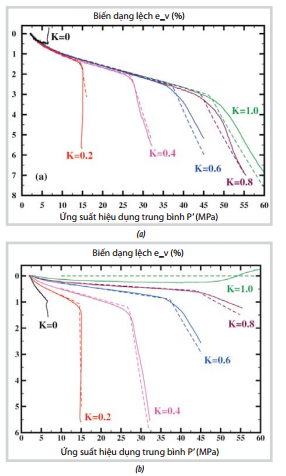 |
| Hình 13. Mô hình đàn hồi - dẻo (đường nét
đứt) so sánh với kết quả thí nghiệm (đường liền) đối với kết quả thí
nghiệm của nhóm mẫu 1: biến dạng thể tích (a); biến dạng lệch (b) |
Trên cơ sở xác định các hệ số bằng thí nghiệm, module và sự thay đổi độ biến dạng đối với tất cả các đường chất tải K bằng cách sử dụng các phương trình (3), (4), (5), (6), trong đó tổng biến dạng được xác định bằng tổng số thành phần biến dạng đàn hồi và biến dạng dẻo
Hình 13 thể hiện các số liệu tính toán được biến dạng thể tích và biến dạng lệch theo ứng suất hiệu dụng trung bình, trong đó có so sánh với các số liệu đo thực tế trong phòng thí nghiệm (Hình 9c và 9d). Đối với các đường chất tải đã thí nghiệm, có thể thấy mô hình đàn hồi - dẻo tương đối phù hợp để mô hình hóa ứng xử cơ học đối với vật liệu đã thí nghiệm.
Tuy nhiên, với kết quả mô hình, nhóm tác giả đã sử dụng một tiêu chuẩn trung gian trong việc xác định áp lực giới hạn dựa trên kết quả dữ liệu đo biến dạng và độ thấm để làm mềm mại đoạn chuyển giao trên các đường cong biến dạng. Đường cong mũ giới hạn do các giá trị áp lực giới hạn tạo ra là rộng hơn so với đường cong “ban đầu” đã được xác định bằng giới hạn cơ học (Hình 11), trong đó đường cong giới hạn “ban đầu” được xác định từ tiêu chuẩn giới hạn đường thẳng.
Bằng thực nghiệm, nhóm tác giả nhận thấy vùng chuyển giao từ đàn hồi sang dẻo tương ứng với giá trị biến dạng dẻo (đặc trưng bởi hệ số biến cứng nguội) được biểu hiện bởi đường cong lồi đối với các đường chất tải K = 1,0; K = 0,8 và K = 0,4. Kết quả này tương tự với công bố của Yale [37] khi tiến hành nghiên cứu trên đá carbonate. Tuy nhiên, mô hình khó có thể mô tả được đoạn chuyển giao đàn hồi - dẻo. Vì vậy để mô hình khớp với các số liệu thực nghiệm, Yale cùng các đồng sự đã đề xuất sử dụng mặt mũ giới hạn “trễ” hơn trong mô hình phần tử hữu hạn; vùng ngoài mặt giới hạn này sẽ là biến dạng dẻo gây ra biến cứng nguội. Có thể nhận thấy mô hình mũ này là khác so với lý thuyết cơ học cổ điển vì lý thuyết này quan niệm ngoài vùng giới hạn ngay lập tức vật liệu ứng xử biến cứng nguội. Điểm thú vị khi dùng mô hình đàn hồi - dẻo ở đây là các hệ số H(eo, k, l) có thể được sử dụng để mô hình hóa cho tất cả đường chất tải để dự báo sự thay đổi biến dạng của vật liệu với các thông số vật liệu (Bảng 4).
7. Kết luận
Kết quả chính của nghiên cứu này về ứng xử cơ học của vỉa dầu có độ cố kết kém và qua những lát cắt cát kết Otter Sherwood được lấy từ vết lộ của mỏ dầu Wytch Farm có thể tóm tắt như sau:
Đường cong biến dạng thể tích theo các đường chất tải khác nhau (K < 1) trùng với đường chất tải đẳng hướng “hydrostatic” (K = 1) dưới gia tải giai đoạn đầu và giai đoạn hai khi biến dạng của vật liệu còn coi là đàn hồi; biến dạng là rất lớn khi đường chất tải có hệ số thỏa mãn 0,2 < K < 0,4. Giai đoạn tiếp theo khi biến dạng là dẻo, biến dạng thể tích chứng tỏ mẫu bị nén dưới tác dụng gia tải đối với tất cả đường chất tải đã thí nghiệm, trừ trường hợp K = 0 khi xuất hiện dạng phá hủy giòn với sự xuất hiện của vết nứt. Vùng chuyển của đường cong là hàm số phụ thuộc vào đường chất tải mà đại diện là tham số K, đường cong biến dạng thể tích trở nên trơn hơn khi giá trị K cao và gấp khúc khi giá trị K nhỏ;
Giá trị ứng suất trung bình giới hạn giảm khi đường chất tải đại diện cho trường hợp có độ lệch cao và cả 2 mô hình Cam-clay hiệu chỉnh, mô hình hàm mũ dạng elipse đều thích hợp cho mặt giới hạn dẻo của mẫu;
Độ rỗng của vật liệu không phục hồi được khi xuất hiện biến dạng hoặc tính nén là không đàn hồi; Kích thước lỗ rỗng bị giảm rất nhiều và nhỏ hơn 0,1μm. Độ phân giải của phép đo X-ray không đủ để xác định quá trình phá hủy và xác định vùng phá hủy của đường gia tải K> 0,2; phân tích vi phân của cấu trúc cho phép thiết lập mốiliên hệ giữa tính cơ học và sự thay đổi độ thấm;Tính chất đàn hồi - dẻo của vật liệu có thể mô hình hóađược. Tuy nhiên, tính thay đổi mềm mại khó mô hình được.
Tài liệu tham khảo
1. M.Brignoli, Di Federico. Compaction of unconsolidated sands and stress path effects: Laboratory evidence. Proceedings of the 6th North America Rock Mechanics Symposium, Houston, Texas, US. 5 - 9 June, 2004.
2. G.H.Newman. Pore-volume compressibility of consolidated, friable, and unconsolidated reservoir rocks under hydrostatic loading. Journal of Petroleum Technology. 1973; 25(2): p. 129 - 134.
3. B.R.Crawford, P.F.Sanz, B.Alramahi, N.L.DeDontney. Modeling and prediction of formation compressibility and compactive pore collapse in siliciclastic reservoir rocks. Proceedings of the 45th US. Rock Mechanics/Geomechanics Symposium. San Francisco, US. 26 - 29 June, 2011.
4. J.M.Segura, Q.J.Fisher, A.J.L.Crook, M.Dutko, J.G.Yu, S.Skachkov, D.A.Angus, J.P.Verdon, J-M.Kendall. Reservoir stress path characterization and its implications for fluid- flow production simulations. Petroleum Geoscience. 2011; 17(4): p. 335 - 344.
5. H.Ruistuen, LW.Teufel, D.Rhett. Influence of reservoir stress path on deformation and permeability of weakly cemented sandstone reservoirs. SPE Reservoir Evaluation & Engineering. 1999; 2(3): p. 266 - 272.
6. D.W.Rhett, L.W.Teufel. Effect of reservoir stress path on compressibility and permeability of sandstones. SPE Annual Technical Conference and Exhibition, Washington, US. 4 - 7 October, 1992.
7. C.T.Chang, M.D.Zoback. Viscous rheology and state of stress in unconsolidated sands. SPE/ISRM Rock Mechanics in Petroleum Enginering, Trondheim, Norway. 8 - 10 July, 1998.
8. Teng-fong Wong, Christian David, Wenlu Zhu. The transition from brittle faulting to cataclastic flow in porous sandstone: Mechanical deformation. Journal of Geophysical Research. 1997; 102(B2): p. 3009 - 3025.
9. P.Baud, S.Vinciguerra, C.David, A.Cavallo, E.Walker, T.Reuschlé.Compactionandfailureinhighporositycarbonates: Mechanical data and microstructural observations. Pure & Applied Geophysics. 2009; 166: p. 869 - 898.
10. Jiaxiang Zhang, Teng-fong Wong, Daniel M.Davis. Micromechanics of pressure-induced grain crushing in porous rocks. Journal of Geophysical Research. 1990; 95(B1): p. 341 - 352.
11. Wei Zhu, Patrick Baud, Teng-fong Wong. Micromechanics of cataclastic pore collapse in limestone. Journal of Geophysical Research. 2010; 115(B4).
12. Rune M.Holt. Permeability reduction induced by a non hydrostatic stress field. SPE Formation Evaluation. 1990; 5(4): p. 444 - 448.
13. F.M.R.Ferfera, J.P.Sarda, M.Boutéca, O.Vincké. Experimental study of monophasic permeability changes under various stress paths. International Journal of Rock Mechanics and Mining Sciences. 1997; 34(3 - 4): p. 37.e1- 37.e12.
14. R.M.Ostermeier. Compaction effects on porosity and permeability: Deepwater gulf of Mexico turbidites. Journal of Petroleum Technology. 2001; 53(2): p. 68 - 74.
15. Wenlu Zhu, Laurent G.J.Montési, Teng-fong Wong. A probabilistic damage model of stress-induced permeability anisotropy during cataclastic flow. Journal of Geophysical Research. 2007; 112(B10): p. 1 - 22.
16. B.R.Crawford, D.W.Webb, K.H.Searles. Plastic compaction and anisotropic permeability development in unconsolidated sands with implications for horizontal well performance. Proceedings of the 42nd US. Rock Mechanics Symsposium, San Francisco, US. 29 June - 2 July, 2008.
17. J.Dautriat, N.Gland, S.Youssef, E.Rosenberg, S.Bekri, O.Vizika. Stress-Dependent directional permeabilities of two analog reservoir rocks: A prospective study on contribution of μ-Tomography and pore network models. SPE Reservoir Evaluation & Engineering. 2009; 12(2).
18. M.Bai, F.Meng, S.Green. Improved determination of stress-Dependent permeability for anisotropic formations. SPE-78188-MS, SPE/ISRM Rock Mechanics Conference, Irving, Texas, U.S. 20-23 October, 2002.
19. J.Dautriat, N.Gland, J.Guelard, A.Dimanov, J.Raphanel. Axial and radial permeability evolutions of compressed sandstones: End effects and shear-band induced permeability anisotropy. Pure & Applied Geophysics. 2009; 166: p. 1037 - 1061.
20. R.I.Korsnes, R.Risnes, I.Faldaas, T.Norland. End effects on stress dependent permeability measurements. Tectonophysics. 2006; 426(1 - 2): p. 239 - 251.
21. S.D.Joshi. Horizontal well technology. PennWell Books. 1991.
22. C.Ayan, N.Colley, G.Cowan, E.Ezekwe, M.Wannell, P.Goode, F.Halford, J.Joseph, A.Mongini, J.Pop. Measuring permeability anisotropy: The latest approach. Oilfield Review. 1994; 6(4): p. 24 - 35.
23. B.R.Crawford, M.J.Gooch, D.W.Webb. Textural, controls on constitutive behavior in unconsolidated sands: Micromechanics and cap plasticity. Proceedings of the 6th North America Rock Mechanics Symposium, Houston, Texas, US. 5 - 9 June, 2004.
24. B.R.Crawford, D.Yale, K.Searles, G.Dasari, W.Webb, M.J.Gooch. Plastic compaction and anisotropic permeability evolution in unconsolidated sand. Communication at Euroconference of Rock Physics and Geomechanics, Oléron. 2005.
25. A.Schofield, P.Wroth. Critical state soil mechanics. McGraw-hill. 1968.
26. D.M.Wood. Soil behavior and critical state soilmmechanics. 1st ed. Cambridge: University Press. 1990.
27. Ph.A.Charlez. Rock mechanics: Volume 2 - Petroleum applications. Editions Technip. 1997.
28. R.Whitlow. Basic soil mechanics. 4th ed. Prentice Hall. 2000.
29. J.B.Svendsen, N.R.Hartley. Comparison between outcrop-spectral gamma ray logging and whole rock geochemistry: implications for quantitative reservoir characterisation in continental sequences. Marine and Petroleum Geology. 2001; 18: p. 657 - 670.
30. S.Holloway, A.E.Milodowski, G.E.Strong, G.Warrington. The Sherwood sandstone group (Triassic) of the Wessex basin, Southern England. Proceedings of the Geologists’ Association. 1989; 100(3): p. 383 - 394.
31. P.S.Spencer, K.P.Isaac. Triassic vertebrates from the Otter sandstone formation of Devon, England. Procceding of the Geologists’ Association. 1983; 94(3): p. 267 - 269.
32. A.J.C.Hogg, I.J.Evans, P.F.Harrison, T.Meling, G.S.Smith, S.D.Thompson, G.F.T.Watts. Reservoir management of the Wytch Farm oil field, Dorset, UK: Providing options for growth into later field life. Petroleum Geology Conference Series. 1999; 5: p. 1157 - 1172.
33. M.B.J.Bowman, N.M.Mcclure, D.W.Wilkinson. Wytch Farm oilfield: deterministic reservoir description of the Triassic Sherwood sandstone. Proceedings of the Petroleum Geology of Northwest Europe. 1993: p. 1513 - 1517.
34. W.H.Mark, M.Gregg. Magnetostratigraphy of the Sherwood Sandstone Group (Lower and Middle Triassic), south Devon, UK: Detailed correlation of the marine and non-marine Anisian. Palaeogeography, Palaeoclimatology, Palaeoecology. 2003; 193(2): p. 325 - 348.
35. P.Baud, W.Zhu, T-F.Wong. Failure mode and weakening effect of water on sandstone. Journal of Geophysical Research. 2000; 105(B7): p. 16371 - 16389.
36. M.D.Bolton. The strength and dilatancy of sands. Géotechnique. 1986; 36(1): p. 65 - 78.
37. D.P.Yale, B.Crawford, H.Watt. Plasticity and permeability in carbonates: Dependence on stress path and porosity. SPE/ISRM Rock Mechanics in Petroleum Engineering, Trondheim, Norway. 8 - 10 July, 1998.
Mechanical behaviour of weakly consolidated sandstone
Nguyen Van Hung, Le Phuoc Hao, Bui Tu An
Petrovietnam University
Summary
Mechanical tests under different stress paths (hydrostatic and proportional with constant ratio of vertical to hori- zontal stress rates) have been performed on a weakly cemented layered sandstone, the Otter Sherwood Sandstone, outcrop analog of the Sherwood reservoir of the Wytch Farm oil field (UK). The elastic and plastic deformation re- gimes are well identified and the determined yield stresses are fitted using the modified Cam-clay and Elliptic Cap models for all the observed onsets of plastic yielding.
Key words: Mechanics, weakly consolidated, stress paths, Wytch Farm oilfield, Otter Sherwood sandstone.