Hệ số nén khí hay hệ số lệch khí (hệ số Z) là thông số quan trọng để xác định tính chất nhiệt động của vỉa khí, tỷ trọng khí, độ nhớt khí, độ nén khí, mô phỏng vỉa khí, tính toán cân bằng vật chất, dự đoán PVT cho giếng dầu và khí… Dựa trên dữ liệu từ biểu đồ Standing-Katz, một số phương pháp đã được phát triển để tính hệ số Z [1 - 3]. Dựa trên phương pháp của Mohammadreza Kamyab [4], nhóm tác giả đã tính toán, xác định hệ số Z bằng mạng neural nhân tạo (ANN) với thông số đầu vào gồm áp suất giả giảm và nhiệt độ giả giảm của 5.940 điểm dữ liệu thực nghiệm [5]. Kết quả nghiên cứu cho thấy mô hình này có thể dự đoán chính xác hệ số Z hơn so với các phương pháp khác và có khả năng áp dụng trên phạm vi nhiệt độ giả giảm 1,05 ≤Tpr ≤ 3 và áp suất giả giảm 0,2 ≤Ppr ≤ 15.

Từ khóa: Hệ số nén khí, hệ số Z, MATLAB, mạng neural nhân tạo.

1. Giới thiệu

Khí thiên nhiên là một hỗn hợp đa thành phần, trong đó chủ yếu là methane (CH4), ngoài ra còn có ethane (C2H6), propane (C3H8), carbon dioxide (CO2), nitrogen (N2) và thành phần hydrocarbon nặng hơn [6]. Dự đoán chính xác hệ số Z giúp giải quyết các vấn đề về kỹ thuật dầu khí, thiết kế, phân tích khai thác khí tự nhiên và xử lý hệ thống [7]. Do đó, cần phát triển phương pháp tin cậy để dự đoán hệ số Z từ các thông số như nhiệt độ, áp suất của hỗn hợp khí thiên nhiên.
Trong phương trình khí thực (khí thiên nhiên), hệ số Z có thể nhận được bởi công thức sau [8]:

PV = ZnRT (1)

Với:

P: Áp suất (psia);

V: Thể tích (ft3);

n: Số lượng mol khí tổng (mol);

R: Hằng số khí = 10.732 psia-ft3/lb-mole  oR.

Lý thuyết về trạng thái tương đương [9, 10] chỉ ra, hệ số Z có thể được định nghĩa như một hàm số của áp suất và nhiệt độ giả giảm. Áp suất và nhiệt độ giả giảm được định nghĩa bởi những phương trình sau [8]:

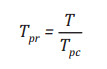(2)

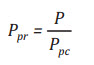(3)

Nhiệt độ giả tới hạn (pseudo critical) Tpc và áp suất giả tới hạn Ppc được tính như sau:

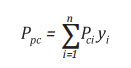(4)

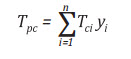(5)

Trong đó:

Pci: Áp suất tới hạn của thành phần i (psia);

T : Nhiệt độ tới hạn của thành phần i (oR);

yi: Phần mol của thành phần i.

Có thể sử dụng biểu đồ Standing và Katz hoặc các phương pháp thực nghiệm để xác định hệ số Z nếu biết thành phần của khí tự nhiên, áp suất và nhiệt độ của khí. Một số nhà nghiên cứu đã tạo ra phương trình toán học để tính hệ số Z phù hợp với biểu đồ Standing và Katz như: Hall và Yarborough [8]; Dranchuk và Abou Kassem [1]; Dranchuk, Purvis và Robinson [2]; Brill và Beggs [3]. Tuy nhiên, những phương trình đó có những hạn chế như: chưa dự đoán chính xác hệ số Z so với dữ liệu thực nghiệm hoặc chỉ dự đoán trong một phạm vi nhất định.

Bài báo này giới thiệu phương pháp tính hệ số Z chính xác bằng cách sử dụng mạng neural nhân tạo với 5.940 điểm dữ liệu thực nghiệm sử dụng phần mềm MATLAB. Mạng neural có thể tính chính xác hệ số Z từ những thông số giả giảm với phạm vi nhiệt độ giả giảm (1,05 ≤ Tpr ≤ 3) và áp suất giả giảm (0,2 ≤ Ppr ≤ 15), như được chứng minh trong nghiên cứu này bởi so sánh kết quả nhận được với những phương pháp khác.

2.Một số phương pháp tính trực tiếp hệ số Z

Có 3 phương pháp ẩn (implicit) phổ biến nhất để tính hệ số Z như sau:

-  Phương pháp Hall và Yarborough [8];
- Phương pháp Dranchuk và Abou-Kassem [1];
- Phương pháp Dranchuk, Purvis và Robinson  [2].

2.2. Phương pháp Hall và Yarborough
 
Phương pháp này là một sự biến đổi của phương trình trạng thái Carnahan-Starling, với các hệ số được phát triển qua sự hồi quy và 1.500 điểm dữ liệu lấy từ biểu đồ hệ số ban đầu của Standing và Katz [8]:

(6)
Với y là nghiệm của phương trình sau:

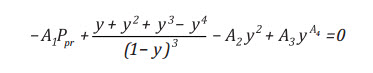(7)

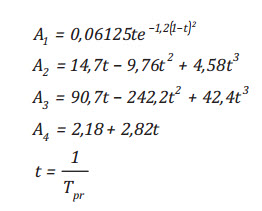
Phương trình (7) là một phương trình không tuyến tính và cần sử dụng kỹ thuật lặp Newton-Raphson hoặc phương pháp chia đôi để giải. Hall và Yarborough chỉ ra rằng phương pháp này không nên áp dụng nếu nhiệt độ giả giảm < 1 [8].

 2.2. Phương pháp Dranchuk và Abou-Kassem

Phương pháp này là một biến đổi 11 hệ số của phương trình trạng thái Benedict-Wedd-Rubin. Những hệ số được tính sử dụng một phương pháp hồi quy với 1.500 điểm dữ liệu lấy từ biểu đồ của Standing và Katz [1]:

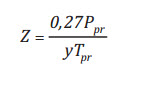(8)

Ppr: Áp suất giả giảm (pseudo-reduced pressure);
Tpr: Nhiệt độ giả giảm (pseudo-reduced temperature);
 y là nghiệm của phương trình sau:
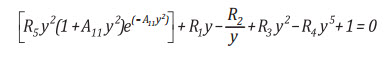(9)

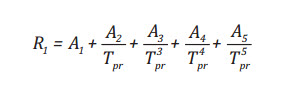
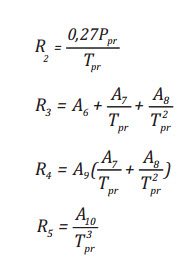
Trong đó A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11 là những hệ số như trong Bảng 1.

Bảng 1. Những hệ số của phương pháp Dranchuk và Abou-Kassem

Phương  trình  (9)  cần  áp  dụng  phương  pháp  lặp Newton-Raphson hoặc phương pháp chia đôi để giải. Phương pháp này được báo cáo là dự đoán hệ số Z từ biểu đồ Standing và Katz với một sai số tuyệt đối trung bình là 0,585% và có thể áp dụng trên phạm vi: 0,2 < Ppr< 15 và 1< Tpr< 3 [8].

2.3. Phương pháp Dranchuk, Purvis và Robinson

Phương pháp này là một biến đổi xa hơn của phương pháp Dranchuk và Abou-Kassem nhận được ban đầu [2]. Phương pháp Dranchuk, Purvis và Robinson có 8 hệ số và cần ít khối lượng tính toán để nhận được hệ số Z.
0, 27 Ppr
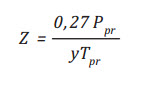 (10)

Trong đó: y là nghiệm của phương trình sau:

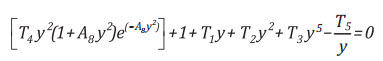  (11)
với

 
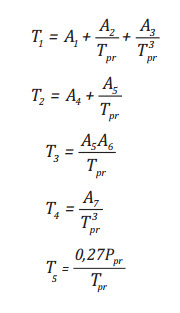
Trong đó A1, A2, A3, A4, A5, A6, A7, A8 là những hệ số như trong Bảng 2.

Bảng 2. Những hệ số của phương pháp Dranchuk, Purvis và Robinson

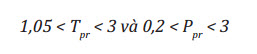
2.4.Các phương pháp khác

Ngoài 3 phương pháp ẩn (implicit) đã nêu còn có những phương pháp hiện (explicit) để tính hệ số Z. Những phương pháp hiện không cần dùng phép lặp để tính hệ số Z nên tránh được vấn đề hội tụ so với phương pháp ẩn. Một trong những phương pháp tốt nhất hiện nay để tính hệ số Z là phương   pháp Beggs và Brill [3]. Gần đây nhiều nhà nghiên cứu đã tìm  ra những phương pháp mới để tính hệ số Z  như:

- Phương pháp Heidaryan, Salarabadi, Moghadasi [7];
- Phương pháp Azizi, Behbahani và Isazadeh [11];
- Phương pháp Sanjari và Lay [12];
- Phương pháp Lateef A.Kareem [13].
 Phương pháp Brill và Beggs  [3]:
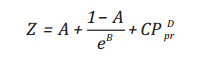 (12)

Với

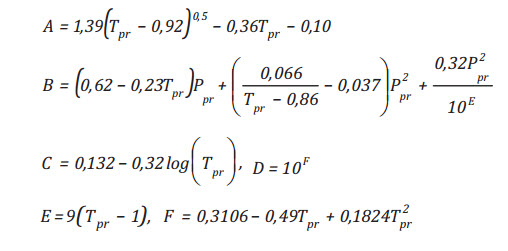
2.5.  Hạn chế của các phương pháp xác định hệ số Z.

2.5.1 Hạn chế của phương pháp hiện

Phương pháp Beggs và Brill khá chính xác trong một phạm vi nào đó, tuy nhiên phương pháp này không được áp dụng khi Tpr < 0,92. Với một vài giá trị của Tpr và Ppr có thể tạo ra giá trị âm của hệ số Z [14].
Phương pháp Heidaryan, Salarabadi, Moghadasi. có hệ số hồi quy 0,99963 nhưng lại không liên tục tại Ppr = 3. Do đó, phương pháp này không được sử dụng để tính hệ số Z tại áp suất giả giảm Ppr = 3. Phương pháp Azizi, Behbahani, Isazadeh chỉ tính hệ số Z trong phạm vi của nhiệt độ giả giảm 1,1 < Tpr ≤ 2 và áp suất giả giảm 0,2 ≤ Ppr ≤ 11. Phương pháp Sanjari và Lay ít hiệu quả so với các phương pháp khác vì hệ số hồi quy là 0,8757 và tỷ lệ sai số tại một điểm nào đó có thể cao tới 90% [13].

2.5.2. Hạn chế của phương pháp ẩn

Các phương pháp ẩn sử dụng phép lặp để giải và đòi hỏi một giả sử trước khi xuất hiện sự hội tụ. Ngoài ra, có một vài trường hợp khi sử dụng những giá trị ban đầu nào đó cho hệ số Z sẽ tạo ra giá trị âm của hệ số Z. Mặc dù có độ chính xác cao nhưng những phương pháp ẩn này có thể không được sử dụng vào một chương trình thiết kế vì nó không thể dự đoán hoặc xác định khi những giá trị sai số đó có thể tạo thành [14].

3. Mô hình mạng neural nhân tạo sử dụng phần mềm MATLAB

3.1. Phần mềm MATLAB

Phần mềm MATLAB được sử dụng trong tất cả những lĩnh vực của toán học ứng dụng, trong giáo dục và nghiên cứu tại các trường đại học và trong giáo dục và nghiên cứu tại các trường đại học và trong công nghiệp. MATLAB (viết tắt của MATrix LABoratory) được xây dựng xung quanh những vector và ma trận. MATLAB    là phần mềm hữu ích cho đại số tuyến tính, là một công cụ tuyệt vời cho việc giải phương trình đạo hàm, phương trình đại số và giải tích số. MATLAB có thể cung cấp những bức ảnh đẹp trong 2D và 3D và là một trong những ngôn ngữ lập trình đơn  giản nhất cho việc viết những chương trình toán học. Ngoài ra, MATLAB cũng hữu ích cho xử lý tín hiệu và ảnh, truyền thông, thiết kế điều khiển tự động, đo lường kiểm tra, phân tích mô hình tài chính, hay tính toán sinh học [15]. Với hàng triệu kĩ sư và nhà khoa học làm việc trong môi trường hàn lâm, MATLAB  là ngôn ngữ của tính toán khoa học.

3.2. Mạng neural nhân tạo

Mạng neural nhân tạo là một hệ thống xử lý thông tin và thử bắt chước chức năng và sự phức tạp của hệ thống neural sinh học [16]. Neural sinh học là một khối cơ sở của hệ thống neural bao gồm 3 phần chính: thân neural (soma), sợi nhánh (dendrite) và sợi trục (axon). Thông tin ở dạng tín hiệu điện được nhận bởi các nhánh, được xử lý bởi thân neural sau đó truyền qua sợi trục. Tương tự, những neural nhân tạo là những khối cơ sở cho mạng neural nhân tạo. Thông tin đến neural nhân tạo qua những đầu vào (input), mỗi đầu vào được nhân bởi một hàm trọng số trước khi đi vào neural. Neural sau đó tổng hợp tất cả dữ liệu đầu vào đã được gia trọng, sai số và xử lý tổng qua một hàm chuyển đổi trước khi truyền thông tin tới những đầu ra [17]. Hình 1 trình bày cấu trúc mạng neural nhân tạo.

Hình 1. Cấu trúc mạng neural nhân tạo [23]

Phương trình sau mô tả hoạt động toán học xảy ra bên trong neural nhân tạo:
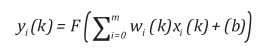(13)
Trong đó:
xi(k) là giá trị đầu vào, wi(k) là giá trị trọng số; trong thời gian rời rạc k (i bắt đầu từ 0 tới m), F là hàm chuyển đổi, b là sai số và yi(k) là giá trị đầu ra trong thời gian rời rạc k [17].
Số lượng những ứng dụng sử dụng ANN rất lớn do ANN có khả năng để xấp xỉ mọi hàm số theo một cách ổn định và hiệu quả. Trong ngành công nghiệp dầu khí, không có một hàm số chính xác hoặc phù hợp để liên kết những thông số đầu vào tới những thông số đầu ra, vì vậy ANN xuất hiện như ứng viên phù hợp để nhận được những mối liên hệ hàm số giữa những thông số đó và kết quả mong muốn [18]. Một số lĩnh vực của công nghiệp dầu khí đã sử dụng thành công ANN như: địa chất và địa vật lý, đánh giá thành hệ và công nghệ mỏ.

Hình 2. Cấu trúc mạng tiến tiếp (feedforward) 2-6-5-1

Bảng 3. Phạm vi của các thông số đầu vào và ra của mạng neural

3.3. Phương pháp thực hiện
3.3.1. Chuẩn bị dữ liệu cho mạng neural

Phải tập hợp và chuẩn bị dữ liệu trước khi bắt đầu quá trình thiết kế mạng. Những dữ liệu đầu vào trong nghiên cứu này là Ppr và Tpr và dữ liệu đầu ra là hệ số Z. Tổng số 5.940 điểm dữ liệu được chọn từ sách công nghệ mỏ khí thiên nhiên được xuất bản bởi SPE [5]. 2/3 dữ liệu được chọn từ tập hợp dữ liệu tổng để thành lập tập dữ liệu đào tạo (training). Một nửa những điểm dữ liệu còn lại được chọn để thiết lập tập dữ liệu phê chuẩn (validation) và phần còn lại là của tập dữ liệu kiểm tra (testing). Những điểm dữ liệu cho mỗi tập hợp được chọn từ tập hợp tổng được phân bố sao cho vẫn giữ được sự đồng nhất giống với tập dữ liệu tổng [15].

3.3.2. Tạo mạng

Sau khi dữ liệu được tập hợp, bước tiếp theo trong đào tạo một mạng là tạo ra một đối tượng mạng. Trong nghiên cứu này, nhóm tác giả sử dụng mạng tiến tiếp (feedforward), một số mạng 1 lớp ẩn (hidden layer) được kiểm tra không đưa ra ứng xử như mong đợi trong toàn  bộ tập dữ liệu với mức độ sai số trên tập phê chuẩn và kiểm tra khá lớn. Qua quá trình nghiên cứu và thử nghiệm, nhóm tác giả đã chọn được mạng 2 lớp ẩn cung cấp kết quả chính xác hơn nhiều so với mạng 1 lớp ẩn. Ngoài ra, những mạng với 3 hoặc nhiều lớp ẩn hơn sẽ chỉ tăng thời gian tính toán mà không cải thiện độ chính xác. Nhóm tác giả sử dụng 6 neural cho lớp ẩn đầu tiên và 5 neural cho lớp ẩn thứ 2 (Hình 2).

3.3.3.Định hình mạng

Tiếp theo là chọn số lượng neural trong mỗi lớp. Số lượng neural nhỏ sẽ đào tạo mạng nhanh hơn nhưng không cho kết quả chính xác. Trong khi đó, tăng số lượng neural có thể tăng thời gian xử lý. Nhóm tác giả sử dụng cấu trúc mạng với 6 neural trong lớp ẩn thứ nhất và 5 neural trong lớp ẩn thứ hai (mạng 2-6-5-1). Hình 2 biểu diễn cấu trúc mạng mô phỏng. Những hàm hoạt động cho những lớp ẩn là hàm tag-sigmoid và log-sigmoid và hàm pure linear được sử dụng cho lớp đầu ra. Những hàm đó được biểu diễn như sau:

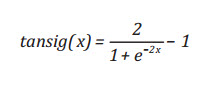
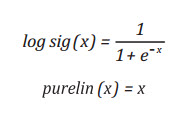
3.3.4. Khởi chạy trọng số và sai số

Trước khi đào tạo một mạng tiến tiếp phải khởi động (thủ công hoặc tự động) những trọng số và những sai số.

3.3.5. Đào tạo mạng

Khi những trọng số và sai số của mạng được khởi động, mạng đã sẵn sàng cho đào tạo. Quá trình đào tạo mạng bao gồm việc điều chỉnh những giá trị trọng số và sai số của mạng để tối ưu hiệu suất mạng. Có 2 cách đào tạo mạng: phương pháp tăng và phương pháp theo đợt. Trong phương pháp tăng, gradient được tính và những trọng số được cập nhật sau khi mỗi đầu vào được áp dụng tới mạng. Trong phương pháp theo đợt, tất cả dữ liệu đầu vào trong tập đào tạo được áp dụng tới mạng trước khi trọng số được cập nhật [15].

Một vài phương pháp đào tạo lan truyền ngược đã tồn tại như thuật toán Levenberg- Marquardt Algorithm (LMA), Scaled Conjugate Gradient (SCG), Pola-Ribiere conjugate gradient (PCG) và những thuật toán khác. Một số nghiên cứu chỉ ra rằng LMA đủ mạnh và cung cấp ANN chính xác [19, 20]. Trong quá trình đào tạo, trọng số được thay đổi bởi thuật toán cho tới khi tổng của những sai số bình phương đủ  nhỏ.

3.3.6. Phân tích hiệu suất mạng neural sau khi đào tạo

Sau khi mạng được đào tạo và đạt tới 1.000 phép lặp có thể thu được đồ thị biểu diễn hiệu suất của quá trình đào tạo như Hình 3.

Hình 3 biểu diễn tổng sai số bình phương cho 3 tập dữ liệu với số lần lặp cho mạng có cấu trúc 2-6-5-1 sử dụng thuật toán đào tạo lan truyền ngược LMA (Levenberg-Marquardt Algorithm). Ứng xử của đường cong thể hiện quá trình đào  tạo thành công và 3 tập dữ liệu được chọn phù hợp từ tập dữ liệu ban đầu. Hiệu suất tốt nhất là MSE = 7.444 x 10-6 tại lần lặp thứ 999. Hình 4 trình bày dữ liệu đào tạo, xác nhận, kiểm  tra  và  dữ  liệu  tổng.  Đường  nét  đứt trong mỗi đồ thị của Hình 4 trình bày kết quả sau khi đào tạo trùng với dữ liệu mục tiêu. Đường nét liền trình bày sự hồi quy tuyến tính tốt nhất giữa kết quả đào tạo và mục tiêu. Giá trị R biểu thị một mối quan hệ giữa kết quả và mục tiêu. Nếu R = 1 thì đó là một mối quan hệ tuyến tính chính xác giữa kết quả đào tạo và mục tiêu [15].
Kết quả của dữ liệu được đào tạo bởi mô hình mạng neural nhân tạo trong nghiên cứu này chỉ ra đây là một mối quan hệ chính xác: kết quả đào tạo, kết quả xác nhận, kiểm tra và kết quả tổng cộng đều có cùng một giá trị R =  0,99997.

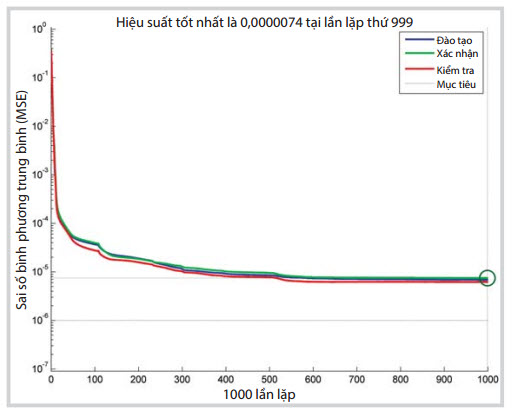Hình 3. Đồ thị biểu diễn hiệu suất của mạng neural nhân tạo 2-6-5-1

Hình 4. Đồ thị hồi quy của mạng neural nhân tạo

3.3.7. Sử dụng mạng

Sau khi mạng được đào tạo với hiệu suất mong muốn có thể sử dụng mô hình đó để xác định hệ số Z. Mô hình dự báo hệ số Z có dạng như sau:

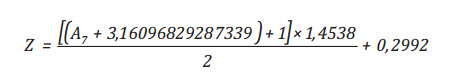(14)

 Với

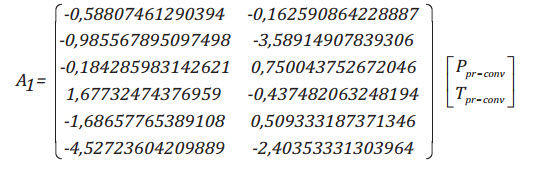
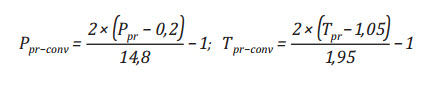
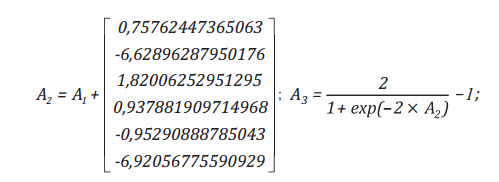
Trong đó:

Ppr-conv: Áp suất giả giảm chuyển đổi trong phạm vi thông số đầu vào;

Tpr-conv: Nhiệt độ giả giảm chuyển đổi trong phạm vi thông số đầu vào.

Đồ thị hệ số Z nhận được từ phương trình (14) được biểu diễn như Hình 5.

4. So sánh sai số của các phương pháp xác định hệ số Z

Để đánh giá sự chính xác của mô hình ANN so với các phương pháp thực nghiệm trước cần sử dụng một số thông số độ lệch thống kê gồm: tỷ lệ sai số tương đối trung bình (APRE - Average percent relative error), sai số  bình  phương  trung  bình (MSE- Mean squared error), căn bậc   hai của sai số bình phương trung bình (RMSE - Root mean squared error), hệ số xác định (R2 - Coefficient of determination).

 Phần trăm sai số tương đối trung bình (APRE hoặc ARE%) đánh giá độ lệch tương đối của dữ liệu hệ số Z được dự đoán và dữ liệu thực tế [21]:

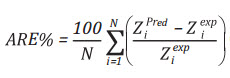
Trong đó:

N: Tổng số các phần tử (5.940 phần tử);

i: Chỉ số phần tử thứ i;

Z Pred: Hệ số Z được dự đoán từ các công thức thực nghiệm hoặc mạng neural nhân tạo;

Zi : Hệ số Z thực nghiệm được SPE công bố.

 Sai số bình phương trung bình (MSE) là một công thức ước lượng đo giá trị bình phương của sai số. Giá trị MSE càng nhỏ thể hiện sự dự đoán càng chính xác (22)
 
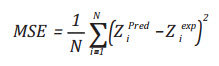(16)
 
Căn bậc hai sai số bình phương trung bình (RMSE) đo dữ liệu rời rạc xung quanh độ lệch 0 (21)

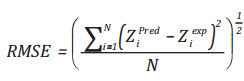(17)
 
Hệ số xác định (R2) là thông số độ lệch thống kê đơn giản trình bày sự phù hợp với dữ liệu [22]:

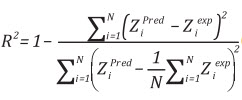(18)
 
 

Hình 5. Đồ thị hệ số Z được tạo ra bởi phương trình (14)

Bảng 4. So sánh những sai số thống kê giữa mô hình ANN và các phương pháp khác

So sánh chất lượng giữa các phương pháp được thể hiện trong Bảng 4 với 5.940 điểm dữ liệu của SPE được sử dụng. Kết quả cho thấy, phương pháp mạng neural nhân tạo có giá trị hệ số xác định (R2) cao nhất: 0,999944 và các sai số thống kê ARE, MSE và RMSE nhỏ nhất. Phương pháp Dranchuk và Abou-Kassem cũng dự đoán hệ số Z khá chính xác với R2 = 0,9996. Phương pháp Brill và Beggs dự báo kém chính xác nhất và không đáng tin cậy khi dự đoán trong phạm vi rộng lớn của áp suất và nhiệt độ giả giảm.

5. Kết luận

Hệ số Z là một thông số rất quan trọng để xác định tỷ trọng khí, độ     nhớt khí, độ nén khí, mô phỏng vỉa khí, tính toán cân bằng vật chất và dự đoán PVT cho giếng dầu và khí. So sánh phương pháp  xác  định  hệ  số  Z theo mô hình dựa trên mạng neural nhân tạo và các phương pháp thực nghiệm khác cho thấy sự vượt trội của phương pháp mới qua các chỉ số    như: hệ số xác định (R2), sai số bình phương trung bình (MSE), căn bậc hai   sai số bình phương trung bình (RMSE), tỷ lệ sai số tương đối trung bình   (ARE) lần lượt là 0,999944, 0,0000036, 0,0019 và 0,0002053. Kết quả này đã chứng minh mô hình mới có thể là công cụ dự đoán chính xác hệ số Z và  có khả năng áp dụng trên phạm vi nhiệt độ và áp suất rộng hơn so với các  phương  pháp khác.
 
Tài liệu tham khảo

1. P.M.Dranchuk, J.H.Abou-Kas- sem. Calculation of Z-factors for natural gases using equations of state. Journal of Canadian Petroleum Technology. 1975; 14(3): p. 34 - 36.

2. R.A.Dranchuk, D.B.Purvis, P.M.Robinson. A reduced equation of state applied to generalized compress- ibility factor tables. Journal of Canadian Petroleum  Technology. 1971.

3. D.H.Beggs, J.P.Brill. An experi- mental study of two-phase flow in in- clined pipes. Journal of Petroleum Tech- nology. 1973; 25(5): p. 607 - 617.

4. Mohammadreza Kamyab, Jorge H.B Sampaio Jr., Farhad Qan- baria, Alfred W.Eustes III. Using artificial neural networks to estimate the z-factor for naturalhydrocarbon gases. Elsevier. 2010.

5. D.L.Katz, D.Cornell.  Handbook of natural gas engineering. New York: McGraw-Hill. 1959.

6. E.Sanjari, E.N.Lay.  Estimation  of natural gas compressibility factors using artificial neural network approach. Journal of Natural Gas Science and En- gineering. 2012; 9: p. 220 - 226.

7. E.Heidaryan, A.Salarabadi, J.Moghadasi. A novel correlation ap- proach for prediction of natural gas com- pressibility factor. Journal of Natural Gas Chemistry. 2010; 19(2): p. 189 - 192.

8. T.Ahmed. Reservoir engineering handbook. Gulf professional publish- ing. 2010.

9. A.Danesh. PVT and phase. Elsevier. 1998.

10. Y.A.Cengel, M.A. Boles. Ther- modynamics: An engineering approach. McGraw Hill. 2007.

11. N.Azizi, R.Behbahani, M.A.Isazadeh. An efficient correlation for calculating compressibility factor of natural gases. Journal of Natural Gas Chemistry. 2010; 19(6): p. 642 - 645.

12. E.Sanjari, E.N.Lay. An accurate empirical correla- tion for predicting natural gas compressibility factors. Joural of Natural Gas Chemistry. 2012; 21(2): p. 184 - 188.

13. L.A.Kareem. New explicit correlation for the com- pressibility factor of natural gas: linearized Z-factor iso- therms. Journal of Petroleum Exploration and Production Technology. 2015; 6(19): p. 1 - 12.

14. K.K.Dune, B.N.Oriji. A new computerized approach to Z-factordetermination. Transnational Journal of Sicience and Technology. 2012; 2(7): p. 64 - 80.

15. M.H.Beale, M.T.Hagan, H.B.Demuth. Neural net- work toolbox user's guide. The MathWorks. 2015.

16. S.Mohaghegh.  Virtual-intelligence  applications in petroleum engineering: Part 1- Artificial neural networks. Journal of Petroleum Technology. 2000; 52(9): p. 64 - 73.

17. K.Suzuki, A.Krenker, J.Bester, A.Kos. Introduction to the artificial neural networks in Artificial neural networks - Methodological advances and biomedical applications. In- Tech. 2011: p. 3 - 18.
 
18. S.Mohaghegh. Neural network: What it  can  do for petroleum engineers. Society of Petroleum Engineers. 1995; 47(1).

19. H.Esen, M.Inalli. Modelling of a vertical ground coupled heat pump system by using artificial neural net- works. Expert Systems with Applications. 2009; 36(7): p. 10229 - 10238.

20. A.Sozen, E.Arcaklioglu, E.G.Kanit. Use of artificial neural networks for mapping of solar potential in Turkey. Applied Energy. 2004; 77(3): p. 273 - 286.

21. A.H.Mohammadi, A.Kamari, F.Gharagheizi. A cor- responding states-based method for the estimation of natu- ral gas compressibility factors. Journal of Molecular Liquids. 2016; 216: p. 25 - 34.

22. M.B.Mohamad, A.Reza, O.Shahriar, Z.Zeinab. Pre- diction of gas compressibility factor using intelligent models. Natural Gas Industry B. 2015; 2(4): p. 283 - 294.

23. Hoàng Anh. Sự trỗi dậy của những cỗ máy. PC World VN. 8/2015.
 
Applying artificial neural networks to predict Z-factor for natural hydrocarbon gas

Tran Kha Tien, Hoang Thinh Nhan
Petrovietnam University Email: tientk01@pvu.edu.vn

Summary

The natural gas compressibility factor or Z-factor is an important parameter to determine thermodynamic prop- erties of gas reservoir, gas density, gas viscosity, gas compression, gas reservoir simulation, calculate the material balance equation, and estimate PVT for oil and gas wells. Based on the data from the Standing-Katz chart, several methods have been developed to calculate the Z-factor [1 - 3]. Based on the method of Mohammadreza Kamyab [4], the authors have calculated and determined the Z-factor using the artificial neural networks (ANN) with input pa- rameters being the pseudo-reduced pressure and temperature of 5,940 experimental data points [5]. The results of research show that this model is able to predict the Z-factor more accurately than other methods and can be applied over the pseudo-reduced temperature range of 1.05 ≤ Tpr ≤ 3 and the pseudo-reduced pressure of 0.2 ≤ Ppr ≤ 15.

Key words: Natural gas compressibility factor, Z-factor, MATLAB, Artificial Neural Networks.