Tóm tắt

Bài báo giới thiệu một hướng tiếp cận để xác định tham số đầu vào cho mô phỏng Monte Carlo (2D) phục vụ dự báo trữ lượng dầu khí dựa trên nghiên cứu mô hình lý thuyết và áp dụng thử nghiệm cho tài liệu thực tế ở mỏ Rạng Đông do Công ty Dầu khí Nhật Việt (JVPC) điều hành.

Từ khóa: Mô phỏng Monte Carlo, tham số đầu vào, độ tin cậy.

1. Mở đầu

Trong công tác dự báo trữ lượng dầu khí, mô phỏng Monte Carlo được sử dụng khá rộng rãi ở các công ty trong và ngoài nước. Tuy nhiên, việc xác định các tham số đầu vào phù hợp luôn được đặt ra cho từng bộ số liệu thu thập được ở mỗi mỏ. Để xác định định lượng các giá trị tham số đầu vào gồm giá trị cận dưới (min), giá trị kỳ vọng (điển hình - most likely) và giá trị cận trên (max) cho mỗi tham số, hiện có hai luồng quan điểm chính về cách xác định gồm:

- a: Sử dụng phân bố giá trị đo được tại giếng khoan ví dụ phân bố độ rỗng từ kết quả minh giải địa vật lý giếng khoan) có trong khu vực mỏ (bước lấy mẫu thường là 0,1 - 0,25m tại giếng khoan);

- b: Sử dụng giá trị trung bình tham số từ từng giếng khoan sau đó tùy thuộc mức độ tin cậy của tài liệu (mật độ giếng khoan…) để lấy cận trên/dưới cho mỗi giá trị tham ố đầu vào.

Với phương án (a), giá trị nhỏ nhất của một tham số (ví dụ độ rỗng…) thường tương ứng với giá trị cutoff (Φ cutoff…) và giá trị cao nhất sẽ tương ứng với giá trị (độ rỗng) lớn nhất có thể gặp tại một điểm độ sâu trong một giếng khoan nào đó. Giả thiết rằng việc tính tham số (độ rỗng…) tại giếng khoan là hoàn toàn chính xác và vỉa chứa không có biến đổi theo diện (chỉ biến đổi theo phương thẳng đứng - mọi giếng khoan đều giống nhau), có nghĩa phân bố giá trị (histogram) ở một giếng khoan sẽ có hình thái giống như với phân bố giá trị khi gộp nhiều giếng khoan lại. Nếu số lượng giếng khoan tiến tới vô cùng thì phân bố giá trị vẫn luôn thu được dải giá trị rộng như khi chỉ có duy nhất một giếng khoan. Điều này không phù hợp vì khi có vô cùng nhiều giếng khoan thì các giá trị cận trên - cận dưới (ví dụ P10, P90) phải trùng với giá trị trung bình từ tất cả các giếng của tham số đó tương ứng với không còn sai số khi tính tham số (độ rỗng…) tầng chứa. Như vậy, việc dùng phân bố giá trị của một tham số từ kết quả giếnkhoan (phương án (a)) là không phù hợp - điều này cũng được khẳng định tại tài liệu hướng dẫn của SPE [1]. Việc xác định định lượng các tham số đầu vào cho mô phỏng Monte Carlo như phương án (b) cần nghiên cứu cho mỗi bộ số liệu cụ thể ở từng khu vực mỏ khác nhau.

2. Phương pháp nghiên cứu

Phương pháp nghiên cứu xác định tham số đầu vào cho mô phỏng Monte Carlo dựa trên mô hình hóa đối tượng/tham số nghiên cứu để xác định miền giá trị của tham số làm cơ sở áp dụng vào điều kiện thực tế.

3. Xây dựng mô hình lý thuyết và giải quyết bài toán

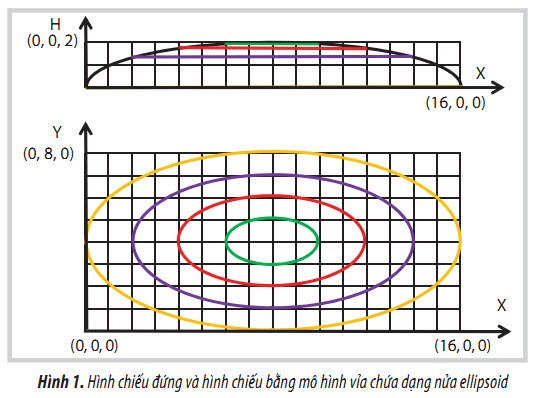
Dưới đây là mô hình lý thuyết về một tham số thử nghiệm là chiều dày vỉa (tương ứng với thông tin về tham số N/G). Mô hình lý thuyết cho tầng chứa có hình dạng là nửa trên của ellipsoid, hình chiếu đứng và hình chiếu  bằng được biểu diễn như Hình 1. Nếu bán kính theo trục x, y, z lần lượt là Rx, Ry, h có giá trị tương ứng là 8, 4, 2 đơn vị, tâm ellipsoid tại điểm có tọa độ (8, 4, 0) khi đó phương trình biểu diễn độ dày (h) tập đá chứa trong không gian sẽ là:

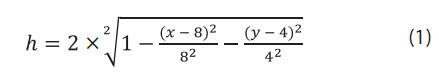
Mỗi cặp giá trị (Xi, Yi) bất kỳ đều cho phép xác định độ dày (h) của tầng chứa theo công thức (1).

Trong thực tế, khi biết được tọa độ giếng khoan và chiều dày tầng chứa qua giếng khoan thì với mạng lưới giếng khoan đủ dày có thể dự báo độ dày (h) ở khu vực chưa khoan (xác suất) bằng nhiều cách khác nhau như:

- Vẽ bản đồ (3D) - phân tích độ nhạy;

- Dùng biểu đồ (2D);

- Dùng phương án “Tam giác giá trị”.

Trong phương pháp 3D (vẽ bản đồ), để xác định sai số (xác suất) có thể gặp cho một tham số khi dự báo có thể tiến hành theo cách đơn giản là thực hiện bỏ một giếng khoan ra khỏi bộ số liệu hiện có (giếng khoan kiểm tra) sau đó vẽ bản đồ dựa trên các thông tin giếng khoan còn lại. So sánh độ lệch của giếng khoan kiểm tra với bản đồ được xây dựng cho phép dự báo sai số có thể gặp tại giếng kiểm tra. Tiến hành tương tự với tất cả các giếng khoan kiểm tra khác trong bộ số liệu với các thuật toán vẽ bản đồ khác nhau cho phép xác định khoảng sai số (xác suất từ phân tích độ nhạy 3D). Dù độ tin cậy tính từ mô hình 3D cao nhưng lại tốn nhiều thời gian, cần dùng phần mềm phức tạp, kiểm soát chặt chẽ tham số đầu vào và không dễ dàng thực hiện.

Dưới đây là đề xuất một tiếp cận đơn giản hơn để xác định cận trên/dưới cho tham số (ví dụ là chiều dày tầng chứa) bằng phương pháp biểu đồ.

Giả thiết một mạng lưới giếng khoan dọc theo đường kinh tuyến và vĩ tuyến (x, y), như vậy mỗi cặp giá trị (Xi, Yi) bất kỳ đều cho phép xác định độ dày h của tầng chứa theo công thức (1). Hình chiếu đứng/chiếu cạnh của tọa độ các giếng này sẽ có dạng nửa hình ellipsoid (Hình 2). Bằng cách thực hiện phép giao biểu đồ (A1 hoặc A2) với 1 hoặc B2) cho phép xác định sai số (dải cận trên/dưới) ở tọa độ bất kỳ.

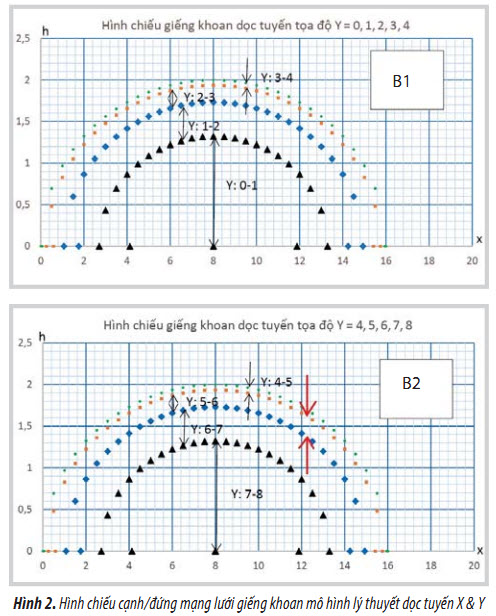
 Ví dụ:

Cần xác định chiều dày tập đá chứa tại điểm có tọa độ (Xi, Yi) là (12,25, 5,3) như vậy giá trị Xi = 12,25 nằm trong dải X = (12 - 14) tương ứng chọn hình 2/A2 và Yi = 5,3 nằm trong dải Y = (5 - 6) tương ứng với Hình 2/B2.

Cách tiến hành xác định chiều dày tại tọa độ (12,25, 5,3):

- Từ Hình 2/A2 lấy giá trị trục hoành là 5,3 gióng lên khoảng X = (12 - 14) và thực hiện tìm dải cận dưới (min) - cận trên (max) của giá trị độ dày h (mũi tên đỏ).

- Từ Hình 2/B2 lấy giá trị trục hoành là 12,25 gióng lên khoảng Y = (5 - 6) và thực hiện tìm dải cận dưới - trên của giá trị độ dày h (mũi tên đỏ).

- Thực hiện phép giao 2 dải cận dưới - cận trên của độ dày h cho kết quả chiều dày h tại tọa độ (12,25, 5,3) cần tìm như trong Bảng 1.

Như vậy nếu tiến hành kiểm tra ở nhiều điểm khác nhau cho phép xác định tham số min - max, trung bình các giá trị min/max của các điểm kiểm tra cho phép xác định dải min - max về chiều dày cần xác định cho mô hình này. Giá trị kỳ vọng theo hướng dẫn của SPE có thể lấy từ trung bình giá trị của các giếng khoan.

Thông qua việc xác định giá trị trung bình tham số của các giếng và trung bình cận trên/dưới cho phép xác định định lượng tham số đầu vào cho mô phỏng Monte Carlo.

Nếu mạng lưới giếng khoan càng dày thì càng có thể thu hẹp khoảng giá trị (X, Y) để chính xác hóa biểu đồ trên Hình 2 tương ứng với việc thu hẹp cận trên/dưới của một tham số quan tâm.

Hạn chế của phương án biểu đồ nêu trên và đề xuất phương án “Tam giác giá trị” để khắc phục:

Việc “dò” giá trị cận trên/dưới dựa trên biểu đồ như trên có hạn chế là phụ thuộc vào chủ quan người thực hiện và khá “vất vả” do vậy để hạn chế sự phụ thuộc này và với sai số ở mức chấp nhận được cũng như đơn giản hóa việc xác định tham số ta có thể lấy giá trị cận trên ứng với giá trị lớn ở giếng khoan trên dải cận trên và giá trị cận dưới ứng với giá trị giếng gần ở dải cận dưới.

Với cách làm này, bài toán trở về dạng đơn giản là trong tam giác xác định bởi 3 giếng khoan gần nhau, giá trị cận dưới khi nội suy trong tam giác sẽ tương ứng với giá trị tham số nhỏ nhất từ 3 giếng khoan và giá trị cận trên tương ứng với giá trị tham số lớn nhất trong 3 giếng khoan. Ngoài ra việc lấy giá trị trung bình từ các giếng khoan làm giá trị đầu vào ứng với giá trị kỳ vọng (như hướng dẫn của SPE) sẽ gặp sai số lớn khi mạng lưới giếng khoan không đều (các giếng khoan gần nhau sẽ chiếm ưu thế khi tiến hành lấy trung bình số học - đây là điều thường xảy ra trong thực tế). Dưới đây là đề xuất các bước xác định tham số cận dưới, cận trên cũng như giá trị kỳ vọng phù hợp cho điều kiện thực tế:

+ Vẽ mạng lưới tam giác xác định bởi từng bộ 3 giếng khoan gần nhau nhất và đánh số từ 1... n;

+ Xác định giá trị tham số lớn/nhỏ nhất ứng với mỗi giếng trong ba giếng khoan. Giá trị này sẽ ứng với cận trên/dưới đại diện cho dải giá trị có thể gặp khi nội suy các điểm phía trong tam giác. Khi đó ta sẽ nhận được bộ giá trị tham số cận dưới/trên cho n tam giác là (min1 … minn) và (max1 … maxn);

+ Xác định diện tích mỗi tam giác (S1 … Sn);

+ Trung bình các giá trị cận dưới/trên từ tất cả các tam giác theo trọng số diện tích tam giác để nhận giá trị cận trên và dưới cho tham số (ví dụ độ rỗng Φ) theo công thức:

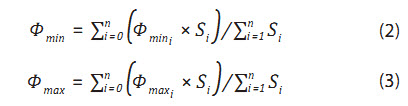
Trong đó  Fmini, Fmaxi là độ rỗng trung bình nhỏ nhất và lớn nhất trong 3 giếng khoan xác định tam giác thứ i.

 Fmini, Fmaxi  là giá trị độ rỗng xác định cận dưới/trên cho mô phỏng Monte Carlo.

Nếu gọi h1, h2, h3 là chiều dày (hiệu dụng - reservoir) tập vỉa ứng với 3 giếng khoan xác định đỉnh một tam giác (thứ i), độ rỗng hiệu dụng trung bình tập tương ứng tại từng giếng khoan này lần lượt là Φ1, Φ2, Φ3, khi đó độ rỗng trung bình đại diện cho tam giác này là Φi = (Φ1 x h1 + Φ2 x h2 + Φ3 x h3)/(h1 + h2 + h3) như vậy độ rỗng trung bình (Φavr) từ các giếng được xác định bằng công thức:

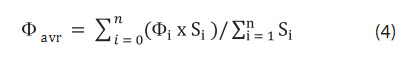
- Công thức (4) có điều chỉnh so với hướng dẫn SPE khi đưa trọng số diện tích tam giác vào để hạn chế ảnh hưởng do mạng lưới giếng khoan không đều và được dùng làm giá trị đầu vào ứng với kỳ vọng mô phỏng Monte Carlo.

Rõ ràng với phương án “Tam giác giá trị” này, trong một số trường hợp sai số lớn hơn so với thực hiện “cẩn thận” và “chăm chỉ” từ phương án biểu đồ 2D nhưng lại phù hợp với việc xác định tham số đầu vào của mô phỏng Monte Carlo 2D thông dụng. Dễ dàng nhận thấy khi lượng giếng khoan tăng lên các giá trị (min, max, most likely) sẽ tiệm cận về giá trị bằng phân tích độ nhạy theo mô hình 3D.

Tương tự ta có thể xây dựng công thức cho tham số tỷ số chiều dày hiệu dụng trên chiều dày chung (N2G) và độ bão hòa nước (Sw):

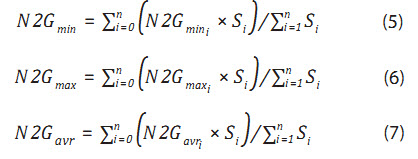
Trong đó:

N2Gmini, N2Gmaxi là tỷ số chiều dày hiệu dụng (reservoir) và chiều dày chung nhỏ nhất và lớn nhất trong 3 giếng khoan xác định tam giác thứ i. N2Gmin, N2Gmax, N2Gavr là giá trị tỷ số chiều dày hiệu dụng và chiều dày chung xác định cận dưới/trên và kỳ vọng cho mô phỏng Monte Carlo.

N2Gavri là chiều dày hiệu dụng trung bình từ 3 giếng khoan xác định đỉnh tam giác thứ i tính theo công thức:

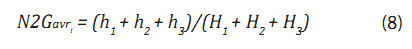
Với h1, H1, h2, H2, h3, H3 lần lượt là chiều dày hiệu dụng và chiều dày tổng của tầng chứa gặp ở các giếng khoan xác định 3 đỉnh tam giác 1, 2, 3.

Và:

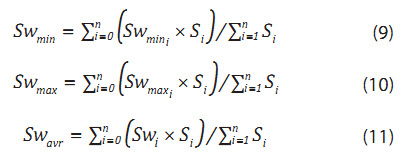
Swmini, Swmaxi là độ bão hòa nước nhỏ nhất và lớn nhất trong 3 giếng khoan xác định tam giác thứ i. Swmin, Swmax, Swavr là giá trị độ bão hòa nước xác định cận dưới/trên và kỳ vọng cho mô phỏng Monte Carlo.

Swi là độ bão hòa nước trung bình từ 3 giếng khoan xác định đỉnh tam giác thứ i tính theo công thức:

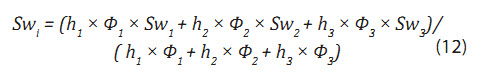
Trong đó: h1, Φ1, Sw1, h2, Φ2, Sw2, h3, Φ3, Sw3 lần lượt là chiều dày hiệu dụng (Pay), độ rỗng hiệu dụng và và độ bão hòa nước trong khoảng hiệu dụng chứa sản phẩm trung bình tại lần lượt ở các giếng khoan xác định 3 đỉnh tam giác 1, 2, 3.

4. Áp dụng thử nghiệm cho tham số độ rỗng từ kết quả giếng khoan mỏ Rạng Đông

Giả sử tam giác ABC tọa độ đỉnh tam giác lần lượt là (XA, YA), (XB, YB) và (XC, YC) khi đó diện tích tam giác ABC xác định theo công thức:

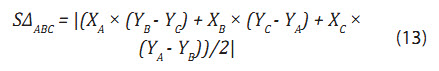
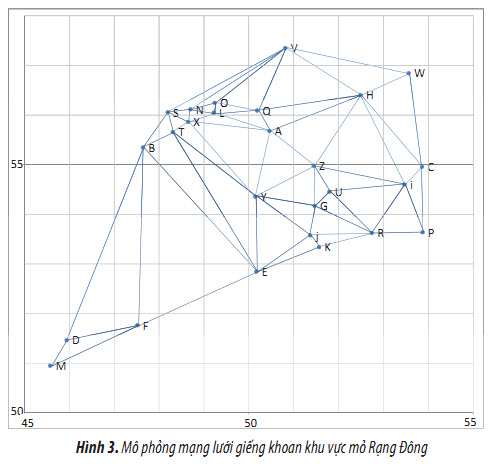
Dưới đây là mô phỏng mạng lưới giếng khoan và mạng lưới tam giác “vẽ thủ công” (Hình 3) cùng bảng tính

giá trị cận trên/dưới và kỳ vọng của tham số độ rỗng theo các công thức (2), (3), (4) (Bảng 2).

Từ bảng tính cho phép xác định các tham số độ rỗng Φmin, Φavr, Φmax:

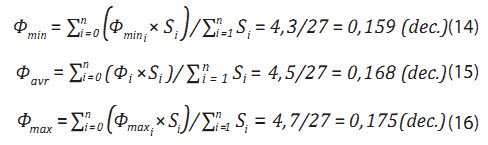
Rõ ràng các tham số độ rỗng min, max, most likely chưa bao gồm sai số có thể gặp tại giếng. Nếu bao gồm cả sai số tại giếng thì cần tiến hành kiểm tra kết quả giếng khoan thông qua 1 trong 2 cách:

- So sánh với kết quả trung bình từ mẫu lõi (Core plug) được lấy cách đều, không chọn lựa.

- Tiến hành phân tích độ nhạy từ công tác xử lý tài liệu tại từng giếng khoan.

Với tài liệu xử lý tốt thì trung bình sai số này chỉ khoảng +/-0,5%, như vậy con số cận trên/dưới để đưa vào mô phỏng Monte Carlo cần bao gồm cả sai số tại giếng khoan nêu trên.

5. Kết luận

Các phân tích, tính toán thử nghiệm nêu trên cũng như dựa trên điều kiện thực tế cho thấy:

- Các tham số trung bình được dùng là tham số kỳ vọng của mô phỏng Monte Carlo tính theo quan điểm ở phương án (a) hay (b) thực tế khác nhau không nhiều, đây cũng là tham số chính liên quan đến dự báo trữ lượng dầu, khí thường được dùng để trình duyệt.

- Tham số min, max trong nhiều trường hợp khác nhau đáng kể và những con số này tuy không ảnh hưởng nhiều đến con số trữ lượng dự báo để trình duyệt nhưng nó lại phản ánh độ tin cậy trong dự báo trữ lượng dầu, khí cũng như mật độ (tương đối) của mạng lưới giếng khoan,hay nói cách khác là sự bất đồng nhất tham số theo diện của tập đá chứa quan tâm…

- Việc sử dụng phương án “Tam giác giá trị” có thể giúp đưa ra con số min/max chấp nhận được để phục vụ công tác dự báo trữ lượng 2D.

Để thuận tiện trong vẽ tam giác, đặc biệt khi lượng giếng khoan nhiều cũng như hạn chế sự phụ thuộc vào chủ quan của con người, nhóm tác giả đã xây dựng phần mềm xác định cận trên, dưới và kỳ vọng thông qua tham số trung bình đá chứa, tọa độ của từng giếng khoan trong khu vực nghiên cứu. Sau khi xác định cận trên/dưới… từ phần mềm này, kết quả cho phép sử dụng tương ứng là tham số đầu vào của mô phỏng Monte Carlo (như phần mềm Crystal Ball) để dự báo trữ lượng dầu khí.

Phần mềm hỗ trợ tính tham số này có thể download tại địa chỉ:

http://www.mediafire.com/download/illr563twm833xe/MonteCarloInputVersion1.0.rar (bao gồm: phần mềm, file hướng dẫn & số liệu mẫu).

Tài liệu tham khảo

1. Society of Petroleum Engineers. Guidelines for application of the petroleum resources management system. November 2011.

2. Đặng Văn Vinh. Bài giảng môn Giải tích hàm nhiều biến. Đại học Bách khoa Tp. Hồ Chí Minh.

3. M.Bern, P.Plassmann. Mesh generation. U.S. Department of Energy, under contract W-31-109-Eng-38.

4. J.Murtha; J.Ross. Uncertainty and the volumetric equation. Society of Petroleum Engineers. Journal of Petroleum Technology. 9/2009; 61 (9): p. 20 - 22.

An approach to define input parameters for Monte Carlo Simulation for HCIIP prediction

Pham Xuan Son - Vietsovpetro;  Dang Duc Nhan - Petrovietnam Exploration Production Corporation (PVEP);  Tran Giang Son - Ho Chi Minh City University of Technology;

Vo Viet Ha - Japan Vietnam Petroleum Corporation (JVPC); Nguyen Viet Hung - Japan Vietnam Petroleum Corporation (JVPC)

Email: sonpx.fg@vietsov.com.vn

Summary

The article brings out an approach to define input parameters for Monte Carlo Simulation to support the prediction of Hydrocarbons Initially in Place (HCIIP) based on theoretical model study and tested with data from Rang Dong oil field operated by Japan Vietnam Petroleum Corporation (JVPC).

Key words: Monte Carlo simulation, input parameters, uncertainty.