Quá trình vận chuyển khí tự nhiên bằng đường ống cao áp, dẫn khí một pha từ nơi khai thác về nơi xử lý được xây dựng mô phỏng thông qua lập trình giải hệ các phương trình mô phỏng một chiều (1D), áp dụng cho lưu chất khí tự nhiên có xem xét chi tiết các thông số đặc tính. Nhóm tác giả sử dụng phương pháp giải tuần tự các phương trình mô phỏng động dòng khí tự nhiên và đề nghị đơn giản hóa phương trình cần giải để giảm thiểu thời gian tính toán, đáp ứng được yêu cầu ứng dụng thực tế công nghiệp. Kết quả thu được trong nghiên cứu này so sánh với kết quả tính toán sử dụng phần mềm thương mại chuyên dụng cho thấy, mô hình xây dựng trong nghiên cứu này có độ sai khác tương đối là 0,41% đối với áp suất, 0,39% đối với lưu lượng và 0,29% đối với nhiệt độ của tuyến ống, đây là 3 thông số quan trọng trong quá trình theo dõi và dự đoán các thông số vận hành tuyến ống dẫn khí 1 pha, sai số cực đại là 3,1%. Sự sai khác này chủ yếu do các giả định vật lý và không do các thuật toán hoặc đề xuất đơn giản hóa mô hình toán học gây ra.
Từ khóa: Vận chuyển khí 1 pha, đường ống dẫn khí cao áp, phương trình trạng thái, mô hình truyền nhiệt, mô phỏng động.
1. Đặt vấn đề
Hiện nay, khí tự nhiên được xem là nguồn năng lượng cho tương lai, là nguồn năng lượng hóa thạch ít gây hiệu ứng nhà kính và các tác động môi trường nhất so với các loại nhiên liệu cùng nguồn gốc. Thành phần của khí tự nhiên chủ yếu là các hydrocarbon và một số ít các tạp chất. Trong quy trình công nghệ xử lý khí tự nhiên, một trong những vấn đề luôn được quan tâm nghiên cứu là tối ưu quá trình vận chuyển khí và phương pháp vận chuyển khí tự nhiên bằng đường ống [1].
Tại Việt Nam, nhu cầu sử dụng khí tự nhiên ngày một tăng cao, lượng khí được cung cấp từ nơi khai thác đến nơi chế biến và tiêu thụ chủ yếu qua hệ thống các đường ống dẫn khí [2]. Với đặc điểm tuyến ống cao áp, việc xác định và đo đạc các thông số trạng thái của khí như áp suất, lưu lượng, nhiệt độ và thành phần khí chỉ có thể thực hiện được tại hai điểm đầu và cuối của tuyến ống. Trong khi đó, quá trình tối ưu, vận hành, dự đoán các tình huống phân phối khí của toàn bộ tuyến ống dẫn khí cần biết đặc tính của dòng khí trên từng điểm theo không gian và thời gian của tuyến ống, sự thay đổi áp suất, lưu lượng và trong một số trường hợp cần biết nhiệt độ của khí trên tuyến ống. Thực tế cho thấy, quá trình đo đạc và xác định thực nghiệm để thu được các dữ liệu này không phải lúc nào cũng thực hiện được, do đó, một trong những phương án được ưu tiên sử dụng là xây dựng mô hình toán học cho phép mô phỏng dự đoán các thông số công nghệ của tuyến ống thông qua các dữ liệu đặc tính của dòng khí tự nhiên và của tuyến ống. Xây dựng mô hình cho phép mô phỏng chính xác quá trình vận chuyển khí tự nhiên trong tuyến ống áp suất cao, chiều dài lớn cũng rất quan trọng trong việc xác định công suất thủy lực của tuyến ống. Khi tuyến ống dẫn khí đã được xây dựng, công suất vận chuyển được xác định thông qua các thông số áp suất đầu vào và đầu ra, cùng với các thông số về dòng chảy của tuyến ống. Kết quả tính toán công suất vận chuyển của ống chính xác sẽ đảm bảo việc tối ưu vận hành và khai thác hệ thống tuyến ống [3].
Mục đích của nghiên cứu này là xây dựng chương trình mô phỏng động, áp dụng mô phỏng dự đoán các thông số gồm lưu lượng, áp suất và nhiệt độ biến đổi theo không gian và thời gian của hệ thống phân phối khí hiện có của Tổng công ty Khí Việt Nam. Trong phạm vi bài báo này, nhóm tác giả giới thiệu kết quả xây dựng bước đầu mô hình toán học cơ sở cho phép mô phỏng hệ thống tuyến ống dẫn khí một pha, cụ thể:
- Áp suất vận chuyển khí đến 200bar, độ dài tuyến ống cho phép đến 400km, đặc tính khí tự nhiên gần giống với khí tự nhiên hiện có của Việt Nam;
- Toàn bộ mô hình mô phỏng được xây dựng sử dụng chương trình MATLAB, có giao diện đơn giản, dễ sử dụng;
- Đề xuất đơn giản hóa các phương trình để đáp ứng thời gian tính toán nhanh, nhưng sai khác không quá 3% so với kết quả thu được từ phần mềm thương mại chuyên dụng đang được ưa chuộng sử dụng để mô phỏng hệ thống đường ống dẫn khí hiện nay. Trong nghiên cứu này, nhóm tác giả so sánh kết quả mô phỏng với phần mềm thương mại như Pipeline Studio.
Mô hình toán học cho phép mô phỏng động tuyến ống dẫn khí được ứng dụng trong theo dõi vận hành tuyến ống dẫn khí tự nhiên. Mô hình này đóng vai trò rất quan trọng trong việc kết hợp hỗ trợ phát hiện rò rỉ của hệ thống. Do đó, xây dựng một mô hình mô phỏng đủ chính xác, tin cậy và thời gian tính toán hợp lý là cần thiết để có thể ứng dụng tính toán liên tục theo hình thức mô phỏng động.
2. Cơ sở lý thuyết xây dựng mô hình - Mô hình dòng chảy 1D
Mô phỏng quá trình vận chuyển khí trên tuyến ống dài và áp suất cao thường được thực hiện thông qua việc giải hệ các phương trình 1D có tính đến quá trình truyền nhiệt của lưu chất khí bị nén và tính đến độ nhớt của khí. Cách giải hệ phương trình này được mô tả chi tiết tại công bố của Thorley và Tiley [4]. Có nhiều phương pháp toán học đã được đề xuất sử dụng để mô phỏng quá trình vận chuyển khí trên đường ống 1 pha. Do tính chất phức tạp của mô hình, thời gian tính toán và độ chính xác của kết quả tính toán luôn cần có sự cân đối, cân nhắc phạm vi ứng dụng. Việc xây dựng mô hình tính toán mô phỏng cho phép thu được kết quả với độ chính xác thích hợp với thời gian nhanh chóng luôn là chủ đề nghiên cứu được xem xét [5].
Trong đó, phương pháp sai phân hữu hạn là phương pháp giải gần đúng cho thời gian tính toán nhanh nhất, kết quả tính toán không sai lệch lớn so với phương pháp giải chi tiết, tuy nhiên bước tính theo thời gian yêu cầu phải rất nhỏ [6, 7]. Để khắc phục nhược điểm này, Poloni [5] đã sử dụng phương pháp Lax-Wendroff, phương pháp giải này cho kết quả ổn định trong ứng dụng mô phỏng này hiện không được ứng dụng rộng rãi do thời gian tính toán lâu và không đáp ứng được yêu cầu công
nghiệp. Bisgaard et al. [8] đã sử dụng phương pháp sai phân hữu hạn đối
với hệ thống đường ống dẫn khí tự nhiên dài 77km, số liệu mô phỏng cho
sai số rất nhỏ so với số liệu thực nghiệm, ưu điểm của phương pháp này
cũng được Osiadacz và Yedroudj chứng minh khi tiến hành so sánh các
phương pháp giải khác nhau ứng dụng cho mô phỏng tuyến ống dẫn khí [9].
Helgaker [6] đã khuyến cáo, khi giải hệ các phương trình khối lượng,
động lượng và năng lượng, có thể giải đồng thời tại thời điểm tức thời,
vì nhiệt độ là thông số phụ thuộc áp suất và tỷ trọng khí, các thông số
này được xác định thông qua mô hình nhiệt động, ví dụ phương trình trạng
thái. Đối lập với phương pháp giải gần đúng, Gato và Henriques [10] đã
đề nghị phương pháp giải chính xác hơn, sử dụng vi phân bậc 3. Phương
pháp này hiện không được ứng dụng rộng rãi do thời gian tính toán không đáp ứng được yêu cầu công nghiệp.
Đến nay, đã có nhiều công bố nghiên cứu về thuật toán và lập trình giải hệ phương trình mô phỏng tuyến ống [11 - 13]. Các nghiên cứu gần đây tập trung vào mô phỏng cải thiện các tính chất vật lý của khí tự nhiên trên tuyến ống hơn là cải thiện phương pháp giải số học [14, 15]. Ví dụ, Langelandsvik [16] đề xuất cải tiến phương pháp dự đoán hệ số ma sát ảnh hưởng đến tổn thất áp suất khi lưu lượng vận chuyển khí lớn, cải thiện khả năng dự đoán lưu lượng tuyến ống thông qua tính toán biến thiên nhiệt độ nước biển theo thời gian và cải thiện công thức tính toán độ nhớt [17], hay cải thiện mô hình truyền nhiệt và dự đoán hệ số truyền nhiệt một cách chính xác hơn [18]. Chaczykowski đã xem xét sự ảnh hưởng việc lựa chọn mô hình nhiệt động đến kết quả tính lưu lượng khí trên tuyến ống [19] và sự ảnh hưởng của mô hình truyền nhiệt tính đến quá trình dự đoán nhiệt độ của môi trường xung quanh tuyến ống [20]. Tuy vậy, áp suất xem xét chỉ giới hạn ở 84bar, trong khi tại Việt Nam, áp suất khí tự nhiên vận chuyển có thể cao hơn 100bar.
2.1 Phương trình dòng chảy
Trên cơ sở tổng hợp các nghiên cứu đã được công bố, nhóm tác giả tiến hành kế thừa và kết hợp các ưu điểm của từng mảng tính toán có trong mô hình. Hệ phương trình cần giải trong mô hình dòng chảy 1 chiều, có tính đến hệ số nén, độ nhớt và truyền nhiệt của lưu chất bên trong ống được tính trung bình trên một diện tích bề mặt ống như sau:
Phương trình dòng chảy (continuity):
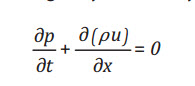 (1)
(1)
Phương trình động lượng (momentum):
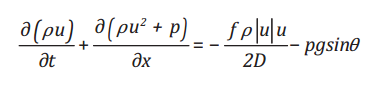 (2)
(2)
Phương trình cân bằng năng lượng (energy):
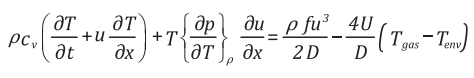 (3)
(3)
Phương trình (1) và (2) được thể hiện ở
dạng bảo toàn, trong khi phương trình (3) có biến đổi nội năng. Phương
trình (2), thành phần đầu tiên của vế phải phương trình là hệ số ma sát
(f ); thành phần thứ hai là góc nghiêng của tuyến ống (sin). Trong
phương trình (3), thành phần thứ nhất của vế trái đặc trưng cho phần
năng lượng chuyển từ năng lượng cơ học thành năng lượng nhiệt; thành
phần thứ 2 đặc trưng cho hiệu ứng Joule-Thomson, là hiệu ứng giảm nhiệt
khi có hiện tượng giãn nở; thành phần cuối của phương trình đặc trưng
cho quá trình trao đổi nhiệt giữa khí tự nhiên và môi trường xung quanh ống, với hệ số truyền nhiệt tổng U (W/m2K) và Tenv là nhiệt độ môi trường, Tgas nhiệt độ dòng khí tự nhiên.
2.1.1. Giải phương trình cân bằng năng lượng
Có thể phân thành 2 nhóm phương pháp giải
phương trình cân bằng năng lượng là phương pháp giải tuần tự và phương
pháp giải đồng thời. Khi tiến hành xây dựng mô hình mô phỏng vấn đề được
quan tâm xem xét là sự tương quan giữa độ chính xác của kết quả thu
được của phương pháp giải và thời gian tính toán cần thiết để thu được
kết quả, khi yêu cầu ứng dụng công nghiệp vừa phải có độ chính xác tương
đối phù hợp nhưng thời gian tính toán không quá dài. Khi so sánh về
thuật toán giải, Helgaker [6] đã kết luận phương pháp giải tuần tự có
thể áp dụng cho việc tính toán mô phỏng tuyến ống dẫn khí 1 pha, cao áp,
dài mà không gây ảnh hưởng lớn đến kết quả mô phỏng. Kết hợp với kết
luận này, nhóm tác giả cũng đề xuất đơn giản hóa một số thành phần có
trong hệ các phương trình thông qua các giả định gần đúng, sử dụng
phương pháp sai phân hữu hạn để giải các phương trình (1), (2) trước,
sau đó giải phương trình (3) và giá trị nhiệt độ sẽ được tính toán cập
nhật cuối cùng.
2.1.2. Mô hình bất đẳng nhiệt toàn phần
Đối với hệ thống đường ống dẫn khí tự
nhiên có đường kính lớn, áp suất vận hành cao, chiều dài lớn đến vài
trăm km, mô hình bất đẳng nhiệt toàn phần thường được lựa chọn vì kết
quả dự đoán biến thiên áp suất và nhiệt độ trên dọc tuyến ống gần với số
liệu thực nghiệm hơn so với các mô hình tính toán khác [21]. Trong quá
trình tính toán mô phỏng vận chuyển khí tự nhiên trên tuyến ống, áp suất
p (bar), lưu lượng khí m (kg/s) và nhiệt độ T (K) là các thông số
thường sử dụng như là biến số. Vi phân theo biến của áp suất, lưu lượng khối lượng được chi tiết như sau:
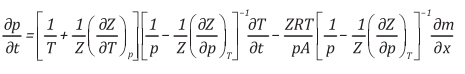 (4)
(4)
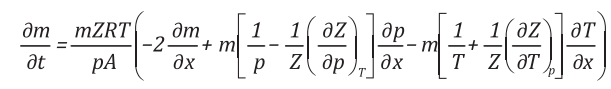 (5)
(5)
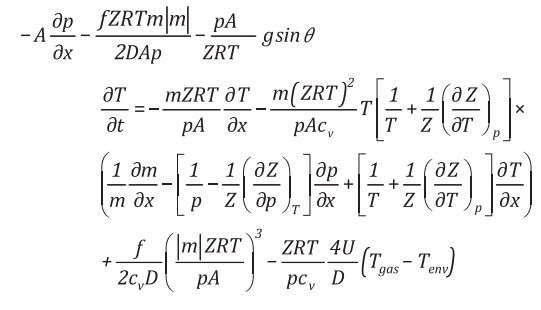 (6)
(6)
Trong đó:
Z: Hệ số nén của khí tự nhiên;
R: Hằng số khí (j/kg × K);
D: Đường kính trong của ống (m);
cv: Nhiệt dung riêng (j/kg × K);
g: Gia tốc trọng trường (m/s2).
Áp dụng
các phương trình tính toán gần đúng sẽ tìm được giá trị nhiệt độ phân bổ
trên toàn bộ đường ống, các giá trị biến số được tính toán theo biến
thiên không gian và thời gian, nếu chọn giá trị biến thiên càng nhỏ thì
kết quả tính toán càng chính xác, đồng nghĩa với thời gian tính toán sẽ
tăng lên.
2.2. Phương pháp tính hệ số ma sát
Hệ số ma sát (f ) tính đến lực ma sát giữa lưu chất khí tự nhiên đi bên
trong ống và bề mặt ống dẫn khí. Hệ số f thường được xác định theo
phương trình Colebrook-White [22] như sau:
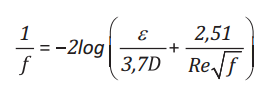 (7)
(7)
Trong đó:
e: Độ nhám bề mặt đường ống;
Re: Chỉ số Reynolds.
Để xác
định hệ số f, phương pháp giải lặp được thực hiện trong mô hình. Nhằm
giảm thời gian tính toán trong mô hình xây dựng, nhóm tác giả sử dụng
phương pháp tính gần đúng hàm toán học có trong chương trình MATLAB.
2.3. Phương trình trạng thái tính toán các thông số đặc tính của khí tự nhiên
Để
tính toán các thông số đặc tính của hỗn hợp khí tự nhiên, quá trình
tính toán cần có các thông số của hỗn hợp khí gồm thành phần của các cấu
tử có trong hỗn hợp khí, các thông số của các cấu tử tinh khiết và điều
kiện nhiệt động. Trong mô hình nhóm tác giả xây dựng, ngoài các
hydrocarbon thường gặp có trong thành phần khí tự nhiên, mô hình cũng áp
dụng cho các hỗn hợp khí tự nhiên chứa các cấu tử nitơ và carbon
dioxide.
Phương trình trạng thái được sử dụng phổ biến nhất trong công nghiệp dầu khí là phương trình Soave-Redlich-Kwong và Peng-Robinson [23]. Theo
nhóm tác giả, đến nay chỉ có Chaczykowski [19] đã nghiên cứu so sánh sự
ảnh hưởng của các mô hình nhiệt động đến quá trình mô phỏng dòng chảy
khí tự nhiên bên trong tuyến ống dẫn
khí 1 pha ở áp suất 84bar và kết luận không có sự sai khác lớn. Mặc dù
vậy, kết quả này có thể không còn chính xác khi áp suất của khí tự nhiên
cao hơn 100bar. Để kiểm chứng và so sánh lựa chọn phương trình trạng
thái phù hợp nhất cho quá trình mô phỏng vận chuyển khí tự nhiên trên
tuyến ống dẫn khí 1 pha tại Việt Nam, cần có nghiên cứu riêng biệt để có
thể kết luận mô hình nhiệt động phù hợp. Với mục tiêu xây dựng mô hình,
nhóm tác giả đã xây dựng cả 2 phương trình trạng thái nêu trên phục vụ
công tác tính toán mô phỏng.
2.3.1. Phương trình SRK
Phương trình Soave-Redlich-Kwong (SRK) [24] được công bố năm 1972, là
phương trình trạng thái có thể mô phỏng chính xác đặc tính nhiệt động
của lưu chất hydrocarbon lên đến áp suất 120bar [23]. Phương trình có
thể viết dưới dạng:
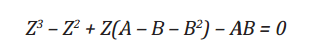 (8)
(8)
Trong đó các thông số A, B là các hàm phụ thuộc của áp suất và nhiệt độ. Z là hệ số nén của khí tự nhiên.
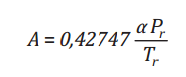 (9)
(9)
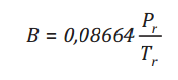 (10)
(10)
Trong đó,
Pr và Tr là tỷ số áp suất và nhiệt độ so với giá trị tới hạn của cấu
tử; là hàm phụ thuộc vào nhiệt độ, nhiệt độ tới hạn và hệ số quay của
cấu tử. Tất cả các thông số cấu tử tinh khiết được mặc định trong chương
trình mô phỏng và lấy theo giá trị khuyến cáo của các phần mềm thương
mại.
2.3.2. Phương trình Peng-Robinson
Phương
trình Peng-Robinson (PR) cũng thuộc nhóm phương trình trạng thái có cấu
trúc gần giống phương trình SRK được đề nghị vào năm 1976 [25], phương
trình này cho kết quả tính toán tỷ trọng pha lỏng chính xác hơn so với
phương trình SRK. Phương trình được biểu diễn dưới dạng:
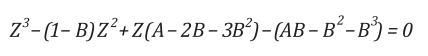 (11)
(11)
Trong đó, các thông số A, B là các hàm phụ thuộc vào áp suất và nhiệt độ;
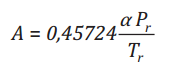 (12)
(12)
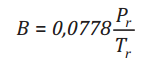 (13)
(13)
Đây cũng
là phương trình nhiệt động được sử dụng rộng rãi trong công nghiệp dầu
khí. Tuy nhiên, phương trình này có sai số lớn khi áp suất lớn hơn
120bar.
3. Mô hình toán học sử dụng
Mô phỏng động cho hệ thống đường ống dẫn khí tự nhiên là việc thực hiện
các tính toán để xác định các giá trị cơ bản như áp suất, lưu lượng và
nhiệt độ trên từng điểm mạng lưới (Node) của đường ống. Trong nghiên cứu
này, phương pháp sai phân hữu hạn được sử dụng để lập trình mô phỏng,
tổ hợp các phương trình dẫn đến phương trình đại số trong thời gian và
không gian rời rạc được biểu diễn như Hình 1. Chiều dài tuyến ống L
(km), được chia thành mạng lưới N điểm, trong đó Δx (x - khoảng cách
không gian (m)) là khoảng cách giữa điểm i và i + 1, với bước thời gian Δt (giây) là khoảng cách từ thời điểm n + 1 so với thời điểm n, khoảng
cách bước không nhất thiết là hằng số mà có thể thay đổi theo cả không
gian và thời gian tùy thuộc vào đặc tính của tuyến ống và đặc tính của
lưu chất đi bên trong ống. Đối với tuyến ống nghiêng, khoảng cách bước
này phải nhỏ hơn so với tuyến ống nằm ngang hoặc không nghiêng.
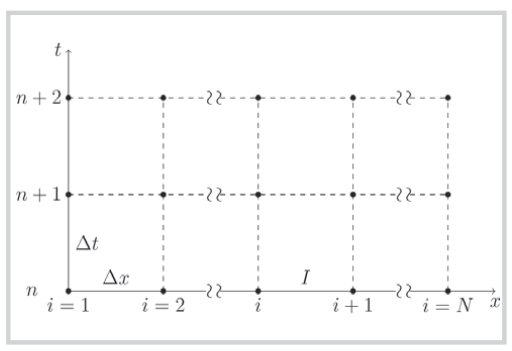 |
| Hình 1. Đường ống được chia thành N điểm
lưới với Δx là khoảng cách giữa điểm i và i + 1, Δt là bước thời gian
giữa thời điểm n + 1 và n |
Việc xác định các biến số cần thiết của hỗn hợp khí tự nhiên di chuyển
trong tuyến ống theo thời gian được xác định theo hai phương pháp sau:
3.1. Phương phápgiảiđiểmmạnglưới tịnh tiếncủa Euler
Euler
đề xuất phương pháp tiêu chuẩn để xác định giá trị lưu lượng tại tất cả
các điểm trên mạng lưới theo thời gian. Vi phân của biến Y tại mạng
lưới điểm i theo thời gian được tính toán gần đúng như sau:
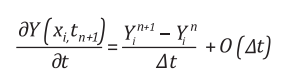 (14)
(14)
Vi phân của biến Y tại điểm i theo không gian được tính gần đúng như sau:
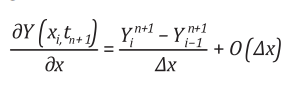 (15)
(15)
Vi phân bậc 2 của biến Y tại điểm i theo không gian được tính gần đúng như sau:
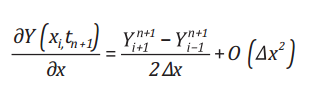 (16)
(16)
Trong đó, Y có thể là biến số m, p hoặc T.
Khi tiến hành giải hệ các phương trình nêu trên, đối với tuyến ống dài
và phức tạp, việc giải hệ các phương trình rất phức tạp với thời gian
tính toán kéo dài. Trong nghiên cứu này, nhóm tác giả kết hợp phương
pháp giải gần đúng của Luskin [26], được gọi là phương pháp mạng lưới
điểm trung tâm.
3.2. Phương pháp mạng lưới điểm trung tâm
Phương
pháp này gần giống với các phương pháp của các tác giả khác [11, 14].
Trong phương pháp này, vi phân riêng phần được tính cho từng đoạn ống mà
không áp dụng riêng cho từng điểm trên mạng lưới ống như phương pháp
của Euler, theo đó, nếu xem xét đoạn ống I (được biểu diễn trên Hình 1 là khoảng từ điểm mạng lưới i đến điểm i + 1). Giá trị vi phân các biến được tính gần đúng như sau:
Vi phân theo thời gian:
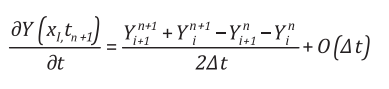 (17)
(17)
Vi phân theo không gian:
 (18)
(18)
Giá trị tức thời của hàm Y được tính theo:
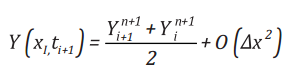 (19)
(19)
Trong trường hợp mô hình không đẳng nhiệt toàn phần, đối với đường ống bao gồm N điểm mạng lưới, có hệ 3 phương trình với 3 biến số tương ứng.
3.3. Đề nghị phương pháp giải và xây dựng mô hình
Ngoài
đề nghị kết hợp đồng thời hai phương pháp giải nêu trên, nhóm tác giả
đề xuất thêm các giả định và đơn giản hóa như dưới đây với mục tiêu giảm
thời gian tính toán nhưng vẫn đảm bảo kết quả mô phỏng không sai khác
nhiều so với kết quả phần mềm chuyên dụng. Ở phạm vi nghiên cứu này,
nhóm tác giả kỳ vọng sai số tương đối không lớn hơn 5%.
Trong
mô hình xây dựng, sau khi cung cấp các thông tin về thành phần khí tự
nhiên, các thông số đặc tính của khí tự nhiên sẽ được tính hoàn toàn sử
dụng phương trình trạng thái, bao gồm cả các giá trị vi phân riêng phần. Thông qua
phương trình trạng thái, tỷ trọng khí tự nhiên, ρ là thông số phụ thuộc
đồng thời vào áp suất và nhiệt độ, được xác định như sau:
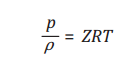 (20)
(20)
Với mục tiêu tiến hành mô phỏng so sánh hệ thống tuyến ống dẫn khí có
áp suất cao hơn 100bar, nhóm tác giả chỉ tiến hành mô phỏng sử dụng
phương trình Soave Redlich Kwong (SRK).
3.4. Đơn giản phương trình dòng chảy và phương trình động lượng
Từ
phương trình động lượng cơ bản (2), tiến hành thay thế các thông số
tính toán thông qua phương trình trạng thái, áp suất và tỷ trọng của khí
tự nhiên liên hệ với vận tốc âm thanh c (m/s) thông qua p = c 2, vế thứ
2 của phương trình này được viết dưới dạng như sau:
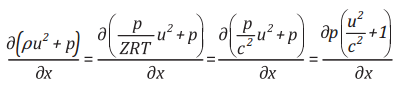 (21)
(21)
Trong thực tế, vận tốc dòng khí tự nhiên di chuyển bên trong tuyến ống có giá trị nhỏ hơn rất nhiều so với vận tốc âm thanh, 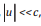 do đó, có thể giả định
do đó, có thể giả định 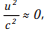 như vậy:
như vậy:
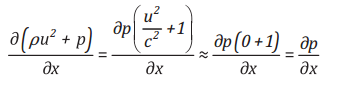 (22)
(22)
Khi tiến hành thay lưu lượng khối lượng
của khí, m (là thông số phụ thuộc vào nhiệt độ và áp suất) thông qua
mối liên hệ với vận tốc dòng khí tự nhiên u (m/s) và diện tích cắt ngang
A (m2) của tuyến ống dẫn khí, m = ρ × u × A, phương trình động lượng
(2) có thể viết lại như sau:
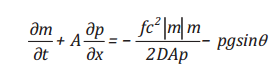 (23)
(23)
Hai phương trình trên chỉ có giá trị là
phi tuyến, để thuận lợi trong việc giải hệ phương trình ta sẽ tuyến
tính hóa giá trị này sang dạng tuyến tính. Theo chuỗi Taylor, một biến
số Y tại thời điểm n + 1 có thể viết lại như sau:
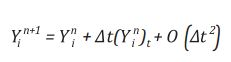 (24)
(24)
Áp dụng công thức này, thành phần đặc trưng cho năng lượng ma sát trong phương trình động lượng được tính gần đúng như sau [26]:
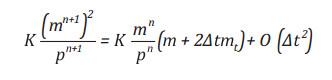 (25)
(25)
Trong đó 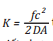 thành phần tính đến năng lượng ma sát có thể viết như sau:
thành phần tính đến năng lượng ma sát có thể viết như sau:
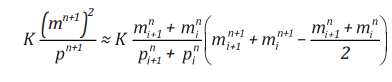 (26)
(26)
Áp dụng
các phương trình tính gần đúng các biến số như trên, đối với đường ống
có N điểm mạng lưới sẽ có 4N biến trong đó có (2N) biến áp suất, (2N)
biến lưu lượng và sẽ có 2 giá trị của điều kiện biên. Để xác định giá
trị của các biến này, có (2N-1) phương trình chuyển tiếp (2 điểm mạng lưới liên tiếp sẽ có 1 phương trình), (2N-1) phương
trình động lượng (2 điểm mạng lưới liên tiếp sẽ có 1 phương trình), khi
tiến hành giải hệ các phương trình này, các biến số áp suất, lưu lượng
tại từng điểm mạng lưới trên toàn tuyến ống được xác định theo thời
gian.
4. Kết quả mô phỏng
Với
mục tiêu xây dựng mô hình có thể mô phỏng động các biến số theo thời
gian và không gian, để hoàn thiện được mô hình cho phép dự đoán chính
xác nhất các biến số quan trọng như áp suất, lưu lượng và nhiệt độ cần
quá trình cải tiến tuần tự. Ở phạm vi nghiên cứu này, nhóm tác giả chỉ
kỳ vọng xây dựng được mô hình với các cải tiến, đơn giản hóa nhưng không
ảnh hưởng nhiều đến kết quả mô phỏng.
4.1. Giao diện chương trình mô phỏng
Mô hình xây dựng trong nghiên cứu này sử dụng chương trình MATLAB với giao diện đơn giản, dự kiến phục vụ mô phỏng hệ thống tuyến ống dẫn
khí của Tổng công ty Khí Việt Nam, các yêu cầu thông số đầu vào giống
như các phần mềm thương mại hiện đang được sử dụng.
Chi tiết các thông số đầu vào của hệ thống tuyến ống dẫn khí vào được
liệt kê trong phần tiếp theo, các thông số chung này cũng được sử dụng
làm thông số đầu vào khi tính toán tuyến ống dẫn khí tự nhiên để tiến
hành so sánh kết quả thu được. Mục tiêu so sánh kết quả tính toán giữa
mô hình xây dựng trong nghiên cứu này với kết quả thu được khi sử dụng
phần mềm thương mại là để kiểm chứng các giả định và phương pháp tính
toán đề xuất.
Theo nhận định của nhóm tác giả khi lập trình xây dựng mô hình, thời
gian tính toán của mô hình xây dựng trong nghiên cứu này giảm xuống
khoảng 20% so với phương pháp giải đồng thời tất cả các phương trình
cùng lúc. Tuy nhiên, việc đánh giá chi tiết khả năng cải thiện thời gian
tính toán không được thực hiện trong nghiên cứu này.
Hình 2. Giao diện phần mềm mô phỏng xây dựng trong nghiên cứu này
4.2. Kết quả so sánh với phần mềm thương mại chuyên dụng
Để
kiểm chứng mô hình xây dựng, nhóm tác giả xem xét hệ thống đường ống
dẫn khí tự nhiên từ nơi khai thác được lắp đặt dưới đáy biển, có chiều
dài 370km, đường kính 0,6604m dẫn vào bờ. Áp suất dòng khí tự nhiên cấp
đầu vào của tuyến ống có giá trị lớn hơn 100bar, giả định nhiệt độ trung
bình của môi trường nước biển là 25oC.
Để
mô tả tuyến ống, nhóm tác giả giả định chia tuyến ống theo từng điểm
mạng lưới, với khoảng cách các điểm mạng lưới là 2km (tương ứng 186
điểm), việc chia các điểm mạng lưới với khoảng cách nhỏ hơn sẽ cho kết
quả mô phỏng động chi tiết và chính xác hơn nhưng thời gian tính toán sẽ
tăng lên. Bước thời gian tính t được chọn trong nghiên cứu này là 60
giây [6].
Các thông số đầu vào của dòng khí tự nhiên và thông tin tuyến ống dẫn khí cụ thể như sau:
- Thành phần khí tự nhiên (% mole):

- Thông số về mạng lưới tuyến ống và số điểm tính trên tuyến ống:
+ Chiều dài đường ống: 370km;
+ Đường kính trong của đường ống, D = 0,6604m;
+ Độ nhám đường ống, Δ = 0,003mm;
+ Hệ số hiệu suất đường ống: 0,925;
+ Khoảng cách giữa 2 điểm mạng lưới: 2km;
+ Bước thời gian tính, Δt = 60 giây.
-
Các thông số giả định về môi trường: nhiệt độ môi trường nước biển
trung bình 25oC với các thông số của điều kiện môi trường nước biển như
sau:
+ Khối lượng riêng của nước: 998,8kg/m3;
+ Độ nhớt, Δ = 1,181cP;
+ Độ dẫn nhiệt: 0,585W/m × K;
+ Vận tốc dòng chảy, u = 0,1m/s;
+ Nhiệt dung riêng, cv = 12kJ/kg × K.
- Thông số tính toán trao đổi nhiệt:
+ Đường ống bọc 3 lớp vật liệu: thép, nhựa đường và bê tông với các thông số như Bảng 1.
Điều
kiện biên: Đa số các hệ thống đường ống vận chuyển khí tự nhiên, lưu
lượng khí cung cấp vào và lấy ra khỏi đường ống là các thông số được
điều khiển. Vì vậy nhóm tác giả sẽ xem xét sự thay đổi của áp suất đầu
vào và ra của hệ thống đường ống với sự biến thiên của lưu lượng đầu vào
và ra trong 240 giờ mô phỏng, tương đương với 10 ngày vận hành thực tế.
Thời gian này đủ để đánh giá mức độ đáp ứng của mô hình nhóm tác giả
xây dựng so với yêu cầu của thực tế công nghiệp. Nhằm đánh giá độ chính
xác của kết quả tính toán giữa mô hình và phần mềm thương mại, nhóm tác
giả đã đề xuất sự biến thiên lớn và thay đổi liên tục của lưu lượng đầu
vào và ra trong khoảng thời gian thực hiện tính toán như Hình 3.
Sau
khi thiết lập điều kiện biên, các thông số gồm áp suất khí đầu vào, áp
suất khí đầu ra và nhiệt độ đầu ra của khí tự nhiên sẽ được tính toán
biến thiên theo thời gian động. Trong phần tiếp theo, nhóm tác giả tiến
hành so sánh sự sai khác giữa kết quả tính toán được bằng mô hình lập
trình trong nghiên cứu này với kết quả dự đoán sử dụng phần mềm thương
mại chuyên dụng, từ đó lựa chọn phương án so sánh sai khác tương đối
(ΔS), theo định nghĩa như sau:
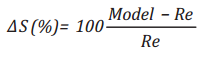 (27)
(27)
Trong đó:
Model: Kết quả tính toán thu được bằng mô hình được lập trình trong nghiên cứu này;
Re: Kết quả thu được sử dụng phần mềm thương mại.
Bảng 1. Thông số về đường ống
Hình 3. Lưu lượng đầu vào/ra đường ống để thực hiện mô phỏng
Hình 4 - 6 lần lượt so sánh kết quả tính toán của mô hình xây dựng trong nghiên cứu này với kết quả thu được khi sử dụng phần mềm thương mại. Các thông số quan trọng nhất đối với quá trình vận hành tuyến ống dẫn khí tự nhiên là lưu lượng (F), áp suất (P) và nhiệt độ (T), toàn bộ các thông số này được tính toán dự đoán biến thiên theo chiều dài của tuyến ống dẫn khí (tại các điểm 0km, 50km, 100km, 150km, 250km, 350km, 370km) và biến thiên theo thời gian (trong khoảng 240 giờ vận hành).
Hình 4. So sánh kết quả tính toán lưu lượng khí tự nhiên sử dụng mô hình được xây dựng trong nghiên cứu này và lưu lượng tính toán sử dụng phần mềm thương mại. Kết quả tính toán tại các điểm khác nhau dọc theo tuyến ống và thay đổi theo thời gian
Hình 5. So sánh kết quả tính toán áp suất
của dòng khí tự nhiên sử dụng mô hình được xây dựng trong nghiên cứu
này và áp suất tính toán sử dụng phần mềm thương mại. Kết quả tính toán
tại các điểm khác nhau dọc theo tuyến ống và thay đổi theo thời gian
Hình 6. So sánh kết quả tính toán nhiệt
độ sử dụng mô hình được xây dựng trong nghiên cứu này và nhiệt độ tính
toán sử dụng phần mềm thương mại. Kết quả tính toán tại các điểm khác
nhau dọc theo tuyến ống và thay đổi theo thời gian.
Hình 7. So sánh kết quả tính toán lưu
lượng (DF), áp suất (DP) và nhiệt độ (DT) sử dụng mô hình được xây dựng
trong nghiên cứu này và kết quả tính toán sử dụng phần mềm thương mại. Sai khác tương đối được biểu diễn tại các điểm biến thiên theo thời gian và không gian
Kết quả
tính toán thu được đối với lưu lượng và áp suất của dòng khí tự nhiên
không thể phân biệt được sự khác nhau giữa kết quả thu được với mô hình
xây dựng trong nghiên cứu này và kết quả thu được sử dụng phần mềm
thương mại chuyên dụng. Tuy nhiên, đối với thông số nhiệt độ, sai khác
này có thể nhận thấy được trên Hình 6. Kết quả này có thể do mô hình
truyền nhiệt nhóm tác giả sử dụng chưa phù hợp hoặc có sự khác nhau lớn
đối với mô hình được sử dụng trong phần mềm thương mại.
Theo
Hình 7, sai khác đối với áp suất khí tự nhiên (DP) trên tuyến ống là
lớn nhất với sai khác trung bình là 0,41% so với kết quả tính toán bằng
phần mềm công nghiệp, sai khác cực đại là -2,6%, sai khác đối với nhiệt
độ của khí tự nhiên (DT) trên toàn tuyến ống là nhỏ nhất với sai khác
tuyệt đối trung bình là 0,29%, sai khác lớn nhất là -2,11%. Mặc dù lưu
lượng khí tự nhiên (DF) là thông số cho kết quả tính toán khá gần so với kết quả tính toán sử dụng phần mềm thương mại, với sai khác tuyệt đối trung bình là 0,39% nhưng sai khác cực đại lại cao nhất với 3,1% tại duy nhất 1 điểm tính toán, sự sai khác này có thể do sự giả định điều kiện vật lý ban đầu đối với tuyến ống.
Nếu công nhận kết quả tính toán thu được bằng phần mềm thương mại là hoàn toàn chính xác so với số liệu thực nghiệm thì kết quả sai khác này hoàn toàn nằm trong giới hạn cho phép khi tiến hành mô phỏng tuyến ống dẫn khí tự nhiên được dẫn từ ngoài khơi, qua hệ thống nước biển vào bờ. Tuy nhiên, với hệ thống tuyến ống dài, việc xây dựng được mô hình tính toán động hệ thống đường ống dẫn khí tự nhiên là rất phức tạp, có rất nhiều yếu tố ảnh hưởng đến kết quả xây dựng mô hình, ngoài ảnh hưởng của thuật toán giải gần đúng thì mô hình nhiệt động, mô hình truyền nhiệt… đều ảnh hưởng đến độ chính xác của quá trình tính toán.
Như vậy, khi tiến hành kiểm chứng kết quả mô phỏng tuyến ống dẫn khí với chiều dài 370km, dẫn khí từ ngoài khơi vào bờ, kết quả so sánh thu được cho phép kết luận: các giả định đơn giản hóa phương trình của nhóm tác giả là hợp lý khi kết hợp với các phương pháp giải gần đúng các hàm vi phân theo thời gian và không gian. Trước khi tiến hành cải tiến các phương pháp dự đoán đặc tính khí tự nhiên, mô hình truyền nhiệt… thì việc tiến hành đánh giá so sánh mức độ chính xác của mô hình hiện tại với kết quả đo đạc thực nghiệm là cần thiết.
5. Kết luận
Vận chuyển khí tự nhiên bằng tuyến ống áp suất cao để dẫn khí từ giàn khai thác ngoài khơi vào đất liền được lập trình mô phỏng sử dụng chương trình MATLAB theo phương pháp giải hệ phương trình 1D. Thông qua việc lập và giải hệ các phương trình, nhóm tác giả đề xuất phương pháp giải gần đúng trên cơ sở kết hợp các phương pháp giải đã được công bố trước đây, giả định đơn giản hóa một số thành phần trong hệ phương trình, điều này cho phép giảm thời gian tính toán nhưng độ chính xác của kết quả phép tính thay đổi không đáng kể (sai số tương đối cực đại không vượt quá 3% so với kết quả thu được bằng phần mềm thương mại). Mô hình tính toán đã được thử nghiệm so sánh đối với tuyến ống dẫn khí 1 pha dài 370km dưới đáy biển, với các giả định cơ bản, kết quả thu được rất gần so với kết quả thu được bởi phần mềm thương mại chuyên dụng.
Trong nghiên cứu này, nhóm tác giả đã tiến hành xây dựng thành công mô hình mô phỏng động quá trình vận chuyển khí tự nhiên trên tuyến ống cao áp, với các giả định đơn giản hóa một số thành phần có trong phương trình, sử dụng phương pháp giải toán tuần tự mô hình này:
- Cho phép mô phỏng động (biến thiên theo không gian và thời gian) hệ thống tuyến ống dẫn khí tự nhiên với chiều dài lên đến 400km, áp suất lên đến 200bar, xử lý được hệ khí tự nhiên có chứa nitơ và carbon dioxide.
- Nếu sai số tính toán đối với áp suất, lưu lượng và nhiệt của khí tự nhiên bên trong tuyến ống thấp hơn 3% là chấp nhận được, mô hình phát triển trong nghiên cứu này có thể đáp ứng được yêu cầu mô phỏng dự đoán phục vụ theo dõi vận hành tuyến ống dẫn khí tự nhiên.
Các kết quả mô phỏng dự đoán sử dụng mô hình xây dựng trong nghiên cứu này sẽ được so sánh với các số liệu thực nghiệm đo đạc trên tuyến ống dẫn khí tự nhiên, đây là yếu tố quyết định trong việc cải tiến các mô hình nhiệt động và mô hình truyền nhiệt cũng như các phương trình khác để nâng cao độ chính xác và tin cậy của chương trình, kết quả này sẽ được đề cập trong công bố sắp tới.
Tài liệu tham khảo
1. R.Z.Ríos-Mercado, C.Borraz-Sánchez. Optimization problems in natural gas transportation systems: A state-of- the-art review. Applied Energy. 2015; 147: p. 536 - 555.
2. Thủ tướng Chính phủ. Phê duyệt Quy hoạch tổng thể phát triển ngành công nghiệp khí Việt Nam giai đoạn đến năm 2015, định hướng đến năm 2025. Quyết định số 459/QĐ-TTg. 30/3/2011.
3. L.I.Langelandsvik, W.Postvoll, B.Aarhus, K.K.Kaste. Accurate calculations of pipeline transport capacity. Proceedings to 24th World Gas Conference, Buenos Aires, Argentina. 2009.
4. A.R.D.Thorley, C.H.Tiley. Unsteady and transient flow of compressible fluids in pipelines - a review of theoretical and some experimental studies. International Journal of Heat and Fluid Flow. 1987; 8(1): p. 3 - 15.
5. M.Poloni, D.E.Winterbone, J.R.Nichols. Comparison of unsteady flow calculations in a pipe by the method of characteristics and the two-step differential Lax-Wendroff method. International Journal of Mechanical Sciences. 1987; 29(5): p. 367 - 378.
6. J.F.Helgaker, T.Ytrehus. Coupling between continuity/momentum and energy equation in 1D gas flow. Energy Procedia. 2012; 26: p. 82 - 89.
7. P.Wang, B.Yu, Y.Deng, Y.Zhao. Comparison study on the accuracy and efficiency of the four forms of hydraulic equation of a natural gas pipeline based on linearized solution. Journal of Natural Gas Science and Engineering. 2015; 22: p. 235 - 244.
8. C.Bisgaard, H.H.Sørensen, S.Spangenberg. A finite element method for transient compressible flow in pipelines. International Journal for Numerical Methods in Fluids. 1987; 7(3): p. 291 - 303.
9. A.J.Osiadacz, M.Yedroudj. A comparison of a finite element method and a finite difference method for transient simulation of a gas pipeline. Applied Mathematical Modelling. 1989; 13(2): p. 79 - 85.
10. L.Gato, J.Henriques. Dynamic behaviour of high- pressure natural-gas flow in pipelines. International Journal of Heat and Fluid Flow. 2005; 26(5): p. 817 - 825.
11. T.Kiuchi. An implicit method for transient gas flows in pipe networks. International Journal of Heat and Fluid Flow. 1994; 15(5): p. 378 - 383.
12. M.Behbahani-Nejad, A.Bagheri. The accuracy and efficiency of a MATLAB-Simulink library for transient flow simulation of gas pipelines and networks. Journal of Petroleum Science and Engineering. 2010; 70(3): p. 256 - 265.
13. G.Greyvenstein. Animplicitmethodfortheanalysis of transient flows in pipe networks. International journal for Numerical Methods in Engineering. 2002; 53(5): p. 1127 - 1143.
14. M.Abbaspour, K.Chapman. Nonisothermal transient flow in natural gas pipeline. Journal of Applied Mechanics. 2008; 75(3).
15. A.J.Osiadacz, M.Chaczykowski. Comparison of isothermal and non-isothermal pipeline gas flow models. Chemical Engineering Journal. 2001; 81(1): p. 41 - 51.
16. L.I.Langelandsvik. Modeling of natural gas transportand friction factor for large-scale pipelines: Laboratory experiments and analysis of operational data. 2008.
17. L.I.Langelandsvik, S.Solvang, M.Rousselet, I.N.Metaxa and M.J.Assael. Dynamicviscositymeasurements of three natural gas mixtures-comparison against prediction models. International Journal of Thermophysics. 2007; 28(4): p. 1120 - 1130.
18. J.Ramsen, S.-E.Losnegard, L.I.Langelandsvik, A.J.Simonsen and W.Postvoll. Important aspects of gas temperature modeling in long subsea pipelines. Pipeline Simulation Interest Group. 2009.
19. M.Chaczykowski. Sensitivity of pipeline gas flow model to the selection of the equation of state. Chemical Engineering Research and Design. 2009; 87(12): p. 1596 - 1603.
20. M.Chaczykowski. Transient flow in natural gas pipeline - The effect of pipeline thermal model. Applied Mathematical Modelling. 2010; 34(4): p. 1051 - 1067.
21. J.F.Helgaker, B.Müller, T.Ytrehus. Transient flow in natural gas pipelines using implicit finite difference schemes. Journal of Offshore Mechanics and Arctic Engineering. 2014; 136(3).
22. C.F.Colebrook, T.Blench, H.Chatley, E.Essex, J.Finniecome, G.Lacey, J.Williamson, and G.Macdonald. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. Journal of the Institution of Civil engineers. 1939; 11(4): p. 133 - 156.
23. J.O.Valderrama. The state of the cubic equations of state. Industrial & Engineering Chemistry Research. 2003; 42(8): p. 1603 - 1618.
24. G.Soave. Equilibrium constants from a modified redlich-kwong equation of state. Chemical Engineering Science. 1972; 27(6): p. 1197 - 1203.
25. D.Y.Peng, D.B.Robinson. A new two-constant equation of state. Industrial & Engineering Chemistry Fundamentals. 1976; 15(1): p. 59 - 64.
26. M.Luskin. An approximation procedure for nonsymmetric, nonlinear hyperbolic systems with integral boundary conditions. SIAM Journal on Numerical Analysis. 1979; 16(1): p. 145 - 164.
Dynamic modelling of transients in high-pressure natural gas pipelines
Nguyen Huynh Duong(1), Nguyen Huynh Dong (2)
1. Petrovietnam Gas Joint Stock Corporation
2. Petrovietnam Manpower Training College
Email: duong.nh1@pvgas.com.vn
Summary
Natural gas is mainly transported undersea in large-scale and long distance pipelines. Prediction of the gas pipeline temperature and pressure profiles is very important in the operation of natural gas transport, especially in case of ac- cidents of pipeline upstream or downstream. An analytical method for calculation of these profiles has been developed and this method of implicit high order finite difference scheme could be a good choice to build the software for simulation of dynamic gas pipeline. In this work, an implicit finite difference scheme has been used to solve the energy equation, the continuity and momentum equation. The flow model was validated by comparing the computed results to commercial software for an offshore natural gas pipeline, with defined natural gas composition. The modelled results showed good agreement with the commercial software (with an average absolute deviation of 0.41% on pressure, 0.39% on flow and 0.29% on temperature).
Key words: Transportation, high-pressure pipelines, equation of state, heat transfer model, dynamic simulation.
Chi tiết bài báo