Trong bài báo này, nhóm tác giả giới thiệu một số mô hình tốc độ cơ học khoan đang được áp dụng để nghiên cứu và nâng cao hiệu quả thi công các giếng khoan tại Việt Nam và trên thế giới.Mô hình “Vietsovpetro” được sử dụng để dự đoán tốc độ cơ học khoan theo thời gian thực cho giếng khoan X mỏ Rồng. Kết quả dự đoán được đánh giá và đối chiếu với kết quả quan sát. Lý thuyết tai biến được áp dụng để giải thích cho sự bất phù hợp giữa kết quả quan sát và kết quả dự đoán tại một số độ sâu. Từ đó mô hình “Vietsovpetro” được cải tiến để giải quyết vấn đề bất phù hợp nêu trên.
Từ khóa: Tốc độ cơ học khoan, choòng khoan, phá hủy đất đá.
1. Các mô hình tốc độ cơ học khoan
Việc xây dựng mô hình tốc độ cơ học khoan rất quan trọng để nghiên cứu đánh giá hiệu quả làm việc của choòng khoan, từ đó xây dựng và hoàn thiện chế độ công nghệ khoan. Các mô hình tốc độ cơ học khoan được nghiên cứu và áp dụng trên thế giới như sau:
1.1 Mô hình Viện Dầu khí Gupkin [1]
Mô hình tốc độ cơ học khoan thường được sử dụng tại Nga có dạng:
Trong đó:
v: Vận tốc tại thời điểm t; v0: Vận tốc ban đầu;
f: Hàm số. Các dạng thường gặp của f là:
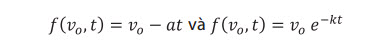 (1)
(1)
với e là cơ số của logarit tự nhiên, a và k là các hằng số được xác định dựa trên kinh nghiệm và thực nghiệm.
Vận tốc cơ học khoan ban đầu được xác định dựa trên một trong các mô hình phổ biến sau:
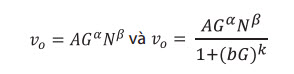
Trong đó:
G: Tải trọng lên choòng;
N: Vận tốc quay của choòng;
A, b, α, β, k: Các hằng số thực nghiệm.
Dạng tổng quát của các mô hình tốc độ cơ học khoan nêu trên được đưa ra dưới dạng [2]:
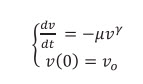 (2)
(2)
với μ ≥ 0 và γ là các hằng số thực nghiệm.
1.2 Mô hình S.A.Shirin-Zade
 |
(3) |
Trong đó:
H: Chiều sâu của giếng;
a, b, c: Các hằng số thực nghiệm.
Mô hình S.A.Shirin-Zade được áp dụng để
nghiên cứu ổn định động lực học quá trình khoan dầu khí tại các giếng
khoan thuộc mỏ Bạch Hổ và mỏ Rồng của Liên doanh Việt - Nga
“Vietsovpetro” [3].
Một số dạng khác của mô hình S.A.Shirin-Zade được trình bày trong một số công trình [4 - 6]
1.3. Mô hình E.M.Galle - H.B.Woods [7]
 |
(4) |
Trong đó:
k: Hằng số đặc trưng cho khả năng khoan qua các lớp đất đá;
ktw: Hằng số đặc trưng cho tính mài mòn răng choòng của đất đá;
k : Tham số thể hiện mức độ ảnh hưởng của độ cứng của đất đá; (k2 = 0,6 đối với đất đá mềm và k2 = 1 đối với đất đá cứng);
tw: Độ mòn của bánh răng choòng;
G: Tải trọng lên choòng;
N: Vận tốc quay của choòng;
p: Hệ số phụ thuộc vào đặc tính hao mòn bánh răng của choòng:
Đối với đất đá cứng, hàm r(N) được xác định theo công thức:
Đối với đất đá mềm:
1.4. Mô hình M.A.Simpson [8]
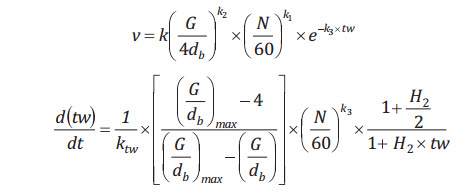 |
(5) |
Trong đó:
db: Đường kính choòng;
ki: Các hằng số (i = 1, 2, 3);
 : Tải trọng lớn nhất (cho phép) lên 1cm đường kính choòng;
: Tải trọng lớn nhất (cho phép) lên 1cm đường kính choòng;
Các hằng số ktw, H2 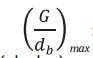 được cho bởi:
được cho bởi:
1.5. Mô hình A.T.Bourgoyne - F.S.Young [9]
Mô hình A.T.Bourgoyne - F.S.Young được biểu diễn bởi phương trình:
Trong đó, 8 thông số ảnh hưởng trực tiếp tới tốc độ khoan được ký hiệu từ a1 tới a8, đó là: sức bền thành hệ, hiệu ứng nén bình thường, hiệu ứng nén không chặt, chênh lệch áp suất, tải trọng lên choòng, tốc độ quay, độ mài mòn răng choòng và ảnh hưởng thủy lực khoan. Công thức đầy đủ miêu tả ảnh hưởng của 8 thông số trên tới tốc độ khoan là:
 là ảnh hưởng của độ bền thành hệ tới tốc độ khoan xuyên;
là ảnh hưởng của độ bền thành hệ tới tốc độ khoan xuyên;
 là ảnh hưởng của hiệu ứng nén lên tốc độ khoan xuyên cơ học, với D, gp lần lượt là độ sâu giếng khoan và gradient áp suất vỉa;
là ảnh hưởng của hiệu ứng nén lên tốc độ khoan xuyên cơ học, với D, gp lần lượt là độ sâu giếng khoan và gradient áp suất vỉa;
 đặc trưng cho chênh lệch áp suất của dung dịch khoan và thành hệ ở đáy giếng;
đặc trưng cho chênh lệch áp suất của dung dịch khoan và thành hệ ở đáy giếng;
 là thông số ảnh hưởng quyết định tới việc phá hủy cục bộ đất đá ở đáy giếng;
là thông số ảnh hưởng quyết định tới việc phá hủy cục bộ đất đá ở đáy giếng; là ngưỡng của tải trọng lên choòng (WOB) mà đất đá bắt đầu bị phá hủy, nằm trong khoảng 0,6 tới 2,0 tùy thuộc vào từng loại đất đá thành hệ;
là ngưỡng của tải trọng lên choòng (WOB) mà đất đá bắt đầu bị phá hủy, nằm trong khoảng 0,6 tới 2,0 tùy thuộc vào từng loại đất đá thành hệ;

là đặc trưng cho ảnh hưởng trực tiếp của tốc độ quay của choòng khoan lên tốc độ khoan cơ học;
 là đặc trưng cho độ mài mòn răng choòng, với h là độ ăn mòn bánh răng choòng;
là đặc trưng cho độ mài mòn răng choòng, với h là độ ăn mòn bánh răng choòng;
 là thông số thủy lực, với ρ là tỷ trọng dung dịch khoan; q là lưu lượng; μ là độ nhớt; dn là đường kính vòi phun.
là thông số thủy lực, với ρ là tỷ trọng dung dịch khoan; q là lưu lượng; μ là độ nhớt; dn là đường kính vòi phun.
1.6. Mô hình “Vietsovpetro” [3]
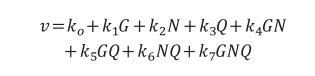 (7) (7) |
Trong đó:
k0, k1, ..., k7: Các hằng số thực nghiệm;
Q: Là lưu lượng dung dịch khoan.
Trong nghiên cứu [3] tác giả đã chỉ ra mô hình“Vietsovpetro” cho các số liệu được lấy từ các giếng khoan tại mỏ Bạch Hổ và mỏ Rồng phù hợp hơn so với các mô hình khác. Gần đây, một dạng khác của mô hình Vietsovpetro” được giới thiệu và áp dụng để nghiên cứu giải pháp công nghệ nâng cao hiệu quả thi công khoan đường kính nhỏ trong thân dầu đá móng nứt nẻ mỏ Bạch Hổ [5]:
 (8) (8) |
2. Kết quả mô phỏng cho mô hình “Vietsovpetro”
Từ thực tế mô hình “Vietsovpetro” thường được áp dụng trong các công tác đánh giá hiệu quả thi công các giếng khoan tại mỏ Bạch Hổ và mỏ Rồng, nhóm tác giả lựa chọn mô hình này để tính toán mô phỏng dự đoán tốc độ cơ học khoan theo thời gian thực từ độ sâu 2.801m tới 2.900m cho giếng X mỏ Rồng.
Nguyên tắc mô phỏng dự đoán tốc độ cơ học khoan theo thời gian thực như sau:
- Lấy 35 bộ số liệu đầu tiên (tương ứng với độ sâu 2.801 - 2.835m) để tính toán các hằng số thực nghiệm cho mô hình. Cỡ mẫu 35 là phù hợp để nghiên cứu theo các công thức tính toán cỡ mẫu hiện nay;
- Sử dụng kết quả tính toán hằng số thực nghiệm ở trên để dự đoán tốc độ cơ học khoan cho mét khoan thứ 2.836;
- Lấy 35 bộ số liệu khoan thực tế tiếp theo (tương ứng với độ sâu 2.802 - 2.836m) để chạy mô phỏng và hiệu chỉnh lại các hệ số cho mô hình;
- Dự đoán tốc độ cơ học khoan cho cho mét khoan thứ 2.837;
- Lặp lại quá trình trên (áp dụng cho mô hình “Vietsovpetro” và mô hình theo (8)) sẽ thu được kết quả như sau:
Trong kết quả mô phỏng được trình bày dưới đây hệ số R2 của từng mô hình (hệ số R bình phương) được đánh giá. Hệ số R2 nhận giá trị trong miền từ 0 đến 1 và được dùng để chỉ “độ khớp” của mô hình so với bộ số liệu quan sát. Cụ thể, ứng với mỗi
35 bộ số liệu dùng để chạy mô phỏng ở trên sẽ có 1 giá trị R2 được tính.
Nếu giá trị R2 càng cao cho thấy mô hình sử dụng để phân tích có khả
năng giải thích càng tốt khác biệt về vận tốc cơ học khoan giữa các quan
sát.
Hình 1 và 3 cho thấy mô hình “Vietsovpetro” có dự đoán tốt hơn so với mô
hình (8). Tuy nhiên, ở cả 2 mô hình trong khoảng độ sâu 2.840- 2.860m đều có hiện tượng sai khác rất lớn giữa giá trị quan sát và giá trị dự báo. Áp dụng phương pháp đánh giá
ổn định động lực học quá trình khoan dầu khí bằng lý thuyết tai biến
được trình bày trong [3, 5, 10], nhóm tác giả thu được kết quả được
trình bày ở Hình 5.
Theo đó, trong khoảng độ sâu 2.840 - 2.860m giá trị Δ tiệm cận 0. Từ lý
thuyết tai biến cho thấy choòng khoan khi khoan trong độ sâu này rơi vào trạng thái kém bền vững, có
tính nhạy cảm cao và mức độ ổn định thấp, trạng thái động học của hệ
thống rất dễ xảy ra các hiện tượng tai biến, dẫn đến sai lệch lớn trong
dự báo vận tốc cơ học khoan. Do vậy, tại những độ sâu mà choòng khoan
làm việc trong trạng thái không ổn định, cần hiệu chỉnh lại mô hình để
công tác dự báo được chính xác hơn.
Hình 1. Dự đoán tốc độ khoan bằng mô hình “Vietsovpetro”
Hình 2. Hệ số R2 của mô hình “Vietsovpetro”
Hình 3. Dự đoán tốc độ khoan bằng mô hình (8)
Hình 4. Hệ số R2 của mô hình (8)
Hình 5. Giá trị Δ theo lý thuyết tai biến
Hình 6. Kết quả mô phỏng theo mô hình “Vietsovpetro” cải tiến
3. Mô hình “Vietsovpetro” cải tiến
Bằng việc đưa thêm giá trị moment xoắn của choòng khoan và giá trị áp suất (vào) của dung dịch khoan để xây dựng mô hình, mô hình vận tốc cơ học khoan được trình bày dưới dạng sau:
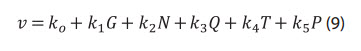
Trong đó:
T (kg × m): Moment xoắn tại choòng;
P (atm): Áp suất (vào) của dung dịch.
Trên thực tế, T và P là các đại lượng có mối liên hệ với G, N, Q bởi các công thức sau [10, 11]:
Với T0 là moment xoắn không phụ thuộc vào tải trọng, sinh ra do ma sát choòng khoan với dung dịch và thành giếng; A là hệ số phụ thuộc đường kính choòng khoan; B là hệ số phụ thuộc vào kích thước giếng khoan, thiết bị trong hệ thống tuần hoàn dung dịch, tính chất lưu biến của dung dịch, đặc tính dòng chảy tại thời điểm xem xét… Vì vậy, về bản chất mô hình (9) có thể được biểu diễn về dạng:
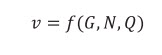
Kết quả xử lý mô phỏng được trình bày trong Hình 6.
Qua các kết quả mô phỏng có thể thấy mô hình “Vietsovpetro” cải tiến luôn có giá trị R2 cao hơn so với mô hình (8) và mô hình “Vietsovpetro”. Bên cạnh đó, trong khoảng độ sâu 2.840 - 2.860m, mô hình “Vietsovpetro” cải tiến cũng thể
hiện sự ổn định hơn so với mô hình “Vietsovpetro” và mô hình (8). Do
đó, giá trị vận tốc cơ học khoan dự đoán trong khoảng độ sâu này của mô
hình “Vietsovpetro” cải tiến chính xác hơn. Điều này được thể hiện thông
qua sai số căn quân phương giữa giá trị quan sát và giá trị dự báo của
3 mô hình trong cùng một khoảng khoan từ 2.840 - 2.860m được trình
bày trong Hình 8.
Hình 7. Giá trị R2 của mô hình “Vietsovpetro” cải tiến.
Hình 8. Sai số căn quân phương của các mô hình cho độ sâu từ 2.840 - 2.860m
4. Kết luận
Bằng việc sử dụng mô hình tốc độ cơ học khoan “Vietsovpetro”, nhóm tác giả đã đưa ra dự đoán tốc độ khoan theo thời gian thực cho giếng khoan X, mỏ Rồng. Kết hợp với kết quả đánh giá ổn định động lực học quá trình khoan từ lý thuyết tai biến, có thể thấy tại những độ sâu mà choòng khoan làm việc ở trạng thái không ổn định, vận tốc cơ học khoan dự đoán có sự sai khác lớn so với thực tế. Từ đó, mô hình “Vietsovpetro” được cải tiến để khắc phục điều này. Kết quả tính toán cho thấy, tại cùng độ sâu mà choòng khoan mất ổn định, mô hình “Vietsovpetro” cải tiến cho kết quả dự đoán với sai số chuẩn chỉ là 1,29 so với sai số chuẩn 3,24 của mô hình ban đầu.
Từ kết quả nghiên cứu, cho phép xây dựng mô hình vận tốc cơ học khoan theo thời gian thực có độ chính xác cao hơn, phù hợp với thực tế thi công xây dựng giếng khoan không những cho các mỏ Bạch Hổ và mỏ Rồng, mà còn cho phép triển khai ở các mỏ khác một cách dễ dàng với mức độ tin cậy cao.
Bằng kết quả của mô hình, cho phép tính toán và xác định được các giá trị thông số công nghệ phù hợp đảm bảo hệ thống khoan luôn hoạt động trong trạng thái ổn định với mức độ bền động lực học cao, cũng như đề xuất được giá trị các thông số công nghệ chế độ khoan tối ưu.
Tài liệu tham khảo
1. Е.К.Юнин. Динамика бурения нефтяных и гозавых скважин. Учебное пособие. УГТУ, Ухта. 2004.
2. В.Г. Григулецкий. Оптимальное управление при бурении скважин. М.: Недра. 1988.
3. Чан Суан Дао. Синергетические принципысовершенствованияиповышения эффективности технологического комплекса буренияскважин на шельфе юга Вьетнама: Дис . Доктора техн. наук. Баку, 2000.
4. Nguyễn Văn Khương, Trần Xuân Đào, Nguyễn Thành Trường. Nghiên cứu, đánh giá trạng thái động học bộ dụng cụ khoan đường kính nhỏ trong móng nứt nẻ mỏ Bạch Hổ. Tạp chí Dầu khí. 2014; 11: trang 18 - 22.
5. Trần Xuân Đào, Nguyễn Thế Vinh. Xác định các thông số chế độ khoan tối ưu bằng cách tiếp cận mới trên quan điểm bền động học của quá trình khoan trong đá móng nứt nẻ - mỏ Bạch Hổ. Tạp chí Dầu khí. 2006; 5: trang 10 - 14.
6. Nguyễn Thế Vinh, Lê Xuân Lân, Trần Xuân Đào. Nghiên cứu và đánh giá trạng thái động học của hệ thống công nghệ khoan dầu khí. Tuyển tập Báo cáo Hội nghị Khoa học - Công nghệ “30 năm Dầu khí Việt Nam - Cơ hội mới, thách thức mới”. Nhà xuất bản Khoa học và Kỹ thuật. 2005: trang 773 - 782.
7. E.M.Galle, H.B.Woods. How to calculate bit weight and rotary speed for lower cost drilling. Oil & Gas Journal. 1960; 58(46): p. 167 - 176.
8. M.A.Simpson. Calculator program optimizes bit weight, rotary speed, reducing drilling cost. Oil & Gas Journal. 1984; 82: p. 71 - 77.
9. A.T.Bourgoyne, F.S.Young. A multiple regression approach to optimal drilling and abnormal pressure detection. Society of Petroleum Engineers Journal. August 1974; 14(4): p. 371 - 384.
10. Trần Xuân Đào. Thiết kế công nghệ khoan các giếng dầu khí. Nhà xuất bản Khoa học và Kỹ thuật. Hà Nội. 2007.
11. А.И.Спивак, А.Н.Попов. Разрушение горных пород при бурении скважин. М.: Недра, Изд.4, перераб. и доп. 1986.
Real time prediction of the rate of penetration (ROP)
Nguyen Van Loi - Petrovietnam University
Tran Xuan Dao - Vietsovpetro
Email: loinv@pvu.edu.vn
Summary
In this paper, the authors recall some ROP models that are used for study and improvement of the efficiency of oil well drilling in Viet Nam and in the world. The ROP model of Vietsovpetro has been used for real time prediction of ROP for well X of Rong oilfield in Viet Nam. The prediction results were evaluated and compared with the real values of ROP. Catastrophe theory is applied for explaining the difference between prediction and real values in an interval of depth where drill bit is in mechanical instability. On that basis, an improvement of the “Vietsovpetro” model is made to tackle the above-mentioned difference.
Key words: Rate of penetration (ROP), drill bit, destruction of rocks.