Tóm tắt
Bài báo giới thiệu một số đánh giá quá trình vật lý dầu tràn trong môi trường biển theo phương pháp mô hình hóa rời rạc trên cơ sở xem xét các quá trình vật lý (như bình lưu, khuếch tán, xáo trộn thẳng đứng và lan truyền ngẫu nhiên). Dựa trên các công thức được áp dụng phổ biến trên thế giới, so sánh kết quả và số liệu phân tích, nhóm tác giả đã xây dựng các phương trình thích hợp để mô phỏng các quá trình vật lý, tính toán các hệ số, tham số hóa các quá trình vật lý môi trường tác động lên dầu tràn và quá trình tương tác ngẫu nhiên của dầu tràn.
Từ khóa: Tràn dầu, các quá trình vật lý, mô phỏng toán học.
1. Giới thiệu
Sự cố tràn dầu gây tác động nghiêm trọng đến môi trường, các hệ sinh thái và kinh tế - xã hội khu vực ven biển. Dầu tràn môi trường tự nhiên dưới tác động của các quá trình sẽ di chuyển từ nơi này đến nơi khác. Các quá trình vật lý bao gồm các quá trình nội lực (tự khuếch tán loang ra ngẫu nhiên) và ngoại lực (thủy động lực môi trường như bình lưu, khuếch tán và xáo trộn thẳng đứng của gió, dòng chảy và sóng)
Khi xảy ra sự cố tràn dầu, dầu chịu tác động của trọng lực loang ra xung quanh, sau đó chịu tác động trực tiếp và chủ yếu của các quá trình thủy động lực biển, trên mặt biển (như gió, dòng chảy mặt, xáo trộn thẳng đứng lớp mặt, sóng…) khiến dầu lan truyền, phân tán ra xung quanh và đi vào trong lớp nước mặt.
Trên cơ sở kết quả nghiên cứu trên thế giới, nhóm tác giả đã tổng hợp và xây dựng các công thức tính toán quá trình bình lưu, quá trình khuếch tán, xáo trộn thẳng đứng và lan truyền ngẫu nhiên... phụ thuộc vào tính chất dầu và tác động của môi trường.
2. Một số quá trình vật lý dầu tràn
2.1. Quá trình bình lưu
Quá trình bình lưu là quá trình cơ học xảy ra do tổng hợp các ảnh hưởng của dòng chảy bề mặt, lực kéo của gió và tác động sóng. Vận tốc trôi của dầu tại bề mặt được xem là tổng của vận tốc gió, sóng và dòng chảy trung bình lớp mặt như sau:
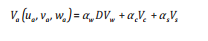 (1)
(1)
Trong đó:
Va(ua, va, wa): Vận tốc trôi dạt của dầu (m/s);
Vw(uw, vw): Vận tốc gió tại độ cao 10m trên mặt nước (m/s);
Vc(uc, vc, wc): Vận tốc dòng chảy trung bình tầng mặt (m/s);
Vs(us, vs, ws): Vận tốc dòng chảy sóng trôi Stokes (m/s); của gió, dòng chảy và sóng).
αw : Hệ số ma sát của gió, thường được chọn bằng 3%[1] và 2,5 - 4,5% [2 - 4];
αc: Hệ số trôi của dòng chảy. thường được chọn bằng 1,1 [5];
αs: Hệ số trôi của sóng, thường được chọn bằng 0,01-0,10 [6];
D: Ma trận chuyển đổi của gió.
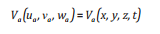 (1a)
(1a)
Để thực hiện chi tiết theo từng thành phần trong trường tốc độ vận chuyển của lan truyền ua, va và wa được xác định theo công thức:
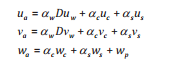 (1b)
(1b)
Trong đó:
uw, vw: Thành phần tốc độ gió 10m (m/s);
uc, vc và wc: Thành phần vận tốc dòng chảy (m/s);
us, vs và ws: Thành phần tốc độ trôi do sóng (m/s);
wp: Thành phần lực nổi.
D là ma trận chuyển đổi của gió được xác định theo [7, 8], như sau:
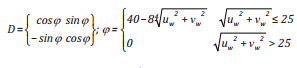 (2a)
(2a)
Dựa trên cơ sở lý thuyết của dòng chảy Ekman {9} và đánh giá tương quan góc lệch (φ) giữa gió và dòng chảy mặt, thay đổi hệ số trôi dạt phụ thuộc vào tốc độ gió thổi được tổng hợp, nhóm tác giả đưa ra các công thức [10], cụ thể:
+ Góc lệch (φ) giữa gió và dòng chảy trôi dạt do gió:
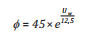 (2b)
(2b)
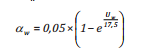 (2c)
(2c)
Hệ số trôi dạt do dòng chảy αc thường được chọn bằng 1,1 [5]. Nhưng thực tế, tốc độ trôi dạt này sẽ bị suy giảm chậm dần hơn so với dòng chảy khi tốc độ dòng chảy môi trường tăng lên. Vậy, dựa trên giá trị của Stolzenbach và nnk [5] và từ kết quả các công trình nghiên cứu trên, nhóm tác giả đã đưa ra công thức liên quan đến xác định hệ số trôi dạt do dòng chảy (thường gọi là hệ số kéo) [10] phụ thuộc vào dòng chảy.
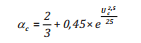 (3)
(3)
Sóng có tác động mạnh tới quá trình lan truyền và phân tán dầu. Việc đưa tác động của sóng vào quá trình lan truyền dầu có thể thông qua dòng chảy trôi Stokes [1] trong sóng:
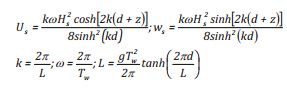 (4a)
(4a)
Từ các công trình nghiên cứu trên, nhóm tác giả đưa ra công thức xác định hệ số trôi do sóng ( s) phụ thuộc vào tốc độ sóng [10], cụ thể:
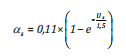 (4b)
(4b)
2.2. Quá trình khuếch tán
Quá trình khuếch tán là quá trình nội lực được tạo ra do tổng hợp các ảnh hưởng của tính chất, đặc điểm của dầu tràn và quá trình trôi dạt quán tính. Tốc độ khuếch tán là tốc độ tổng hợp bao gồm các tính chất, đặc điểm của dầu tràn và ảnh hưởng của ngoại lực (gió, sóng và dòng chảy mặt).
Trong biển, tham số khuếch tán rối ngang có thể dao động trong khoảng từ 0,15m2/s (gần bờ) tới 0,6m2/s (trong cửa sông hẹp với vận tốc dòng chảy khá đáng kể) [11]. Các nghiên cứu thực tế của Okubo [12] về rối biển đã cho thấy các mối quan hệ hữu dụng trong ứng dụng thực tế với quy luật hàm. mũ 4/3 của quan hệ giữa hệ số khuếch tán rối và quy mô độ dài xáo trộn.
Công thức của Fay [13] phụ thuộc vào đặc điểm tính chất dầu (thể tích và mật độ), ảnh hưởng môi trường (mật độ và độ nhớt) và tỷ lệ nghịch với thời gian:
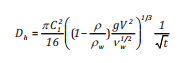 (5)
(5)
Công thức của Proctor và nnk [14] là khuếch tán ngang và thẳng đứng đều phụ thuộc vào tốc độ dòng chảy mặt và gió:
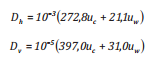 (6)
(6)
Công thức của Johansen [15] phụ thuộc vào đặc điểm tính chất dầu, ảnh hưởng môi trường theo thời gian, phát triển ý tưởng của Fay và chia quá trình khuếch tán thành 2 pha.
Pha 1 với t < 12 giờ:
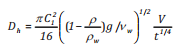 (7a)
(7a)
Pha 2 với t ≥ 12 giờ:
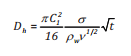 (7b)
(7b)
Công thức của Badri [16] phụ thuộc vào đặc điểm tính chất dầu, ảnh hưởng môi trường và tỷ lệ nghịch với thời gian; khuếch tán thẳng đứng phụ thuộc vào đặc trưng sóng
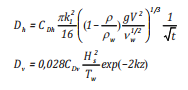 (8)
(8)
Công thức của Tkalich [17], Ehsan và Kourosh [18], Aghajanloo và nnk [19] phụ thuộc vào đặc điểm tính chất dầu (độ dày, mật độ và sức căng bề mặt) và
ảnh hưởng môi trường (mật độ):
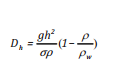 (9)
(9)
Như vậy, khuếch tán ngang phụ thuộc vào đặc điểm tính chất dầu (thể tích, độ dày, mật độ, độ nhớt và sức căng bề mặt) và ảnh hưởng môi trường (mật độ, độ nhớt, sóng, dòng chảy và gió) và thời gian. Tổng hợp các công trình của các nhà khoa học, nhóm tác giả đưa ra hệ thống công thức về tốc độ khuếch tán [10], cụ thể:
+ Tốc độ khuếch tán ngang là:
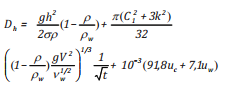 (10a)
(10a)
+ Khuếch tán thẳng đứng phụ thuộc vào đặc trưng sóng, dòng chảy và gió:
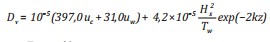 (10b)
(10b)
Trong đó:
Dh và Dv: Tham số khuếch tán ngang và thẳng đứng (m2/s);
C1: Hệ số (0,72);
CDh và CDv: Hệ số tương ứng 3 và 0,015;
g: Gia tốc trọng trường (9,81ms-2);
V: Thể tích dầu (m3);
P và p¬w: Mật độ dầu và nước (kg/m3)
Vw: hệ số nhớt nước (8,9 X 10¬-5 m2/s
σ: Hệ số ứng suất dầu-nước (0,02kgm-2s-1);
uc và uw: Vận tốc dòng chảy và gió (m/s);
H¬s và Tw: Độ cao (m) và chu kỳ (s) sóng;
k: Số sóng (k = 2 / , mà λ là bước sóng hay chiều dài sóng (m));
z: Độ sâu của vị trí hạt tính từ mặt xuống đáy (m);
t: Thời gian (s).
Công thức của Hinze [22], Delvigne và Sweeney [20, 21], Li và Garrett [23] xác định kích thước giọt dầu lớn nhất phụ thuộc tính chất dầu và môi trường:
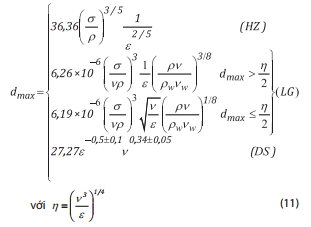 (11)
(11)
Là phổ kích thước giọt dầu phụ thuộc vào thể tích dầu, đường kính giọt dầu và đường kính giới hạn dầu:
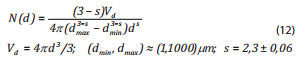 (12)
(12)
Khối lượng phân tán giọt dầu phụ thuộc đặc tính, đường kính giọt dầu và độ cao sóng:
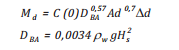 (13)
(13)
2.3. Quá trình xáo trộn dầu và di chuyển thẳng đứng
Sóng có vai trò quan trọng trong tác động làm vỡ lớp dầu trên mặt và chia dầu thành các giọt dầu nhỏ và đi vào trong nước. Lớp xáo trộn do sóng có thể được xem có bậc với độ cao sóng trên mặt. Sóng đổ có thể truyền một năng lượng lớn vào lớp nước mặt biển theo Tkalich và Chan [17]. Các lực tác động lên các giọt dầu nhỏ này bao gồm: khuếch tán thẳng đứng, rối và lực nổi Archimedes. Nếu lực nổi lớn hơn tổng hợp các lực hướng xuống dưới (rối,khuếch tán thẳng đứng) thì giọt dầu sẽ bị nổi lên mặt, nếu không, các giọt dầu sẽ tồn tại trong nước và phân tán đi trong khối nước dưới tác động của dòng mang và khuếch tán rối.
Tuy lượng dầu hòa tan vào nước không lớn và với tốc độ chậm nhưng hậu quả của nó rất lớn, có tác động xấu đến môi trường sinh thái. Dưới tác động của sóng bạc đầu, xáo trộn rối các giọt dầu bị đi vào trong khối nước và hòa tan, biến đổi thể tích của dầu. Về bản chất, dầu hòa vào nước dưới dạng các hạt rất nhỏ bán kính từ 1 - 500μm. Các nghiên cứu thực tế trên biển cho thấy thường dầu đi vào nước có bán kính trung bình khoảng 50 - 70μm [20].
Công thức của Raj [24] là tốc độ thẳng đứng của giọt dầu sẽ phụ thuộc vào trạng thái khối nước và các đặc trưng dầu:
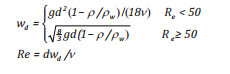 (14)
(14)
Công thức của Delvigne và Sweeney [20], Forrester [25], Spaulding và nnk [26], Proctor và nnk [14] sử dụng giá trị thực nghiệm tới hạn là 50μm, tốc độ nổi và đường kính trung bình phụ thuộc vào trạng thái khối nước và các đặc trưng dầu thông qua giới hạn Reynolds:
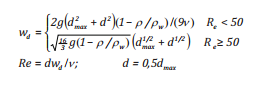 (15)
(15)
Công thức của Aravamudan và nnk [27], Proctor và nnk [14] là tốc độ nổi phụ thuộc vào trạng thái khối nước, các đặc trưng dầu và đường kính giọt dầu chuẩn:
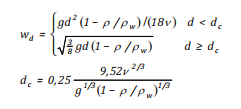 (16)
(16)
Công thức của Kutateladze [28] là tốc độ nổi phụ thuộc vào trạng thái khối nước, các đặc trưng dầu và sức căng bề mặt dầu:
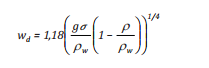 (17)
(17)
Công thức của Tkalich và Chan [17] là tốc độ xáo trộn giọt dầu từ lớp dầu mặt vào trong nước phụ thuộc vào đặc điểm sóng:
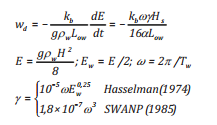 (18)
(18)
Công thức của Delvigne và Sweeney [20], Badri [16] là tốc độ nổi phụ thuộc vào trạng thái khối nước và các đặc trưng dầu:
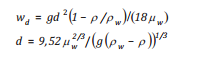 (19)
(19)
Công thức của Al-Rabeh [29], Chao [30], French- -McCay [31], Hai-Long Yin [32] là tốc độ nổi phụ thuộc vào trạng thái khối nước và các đặc trưng dầu và đường kính giọt dầu tới hạn (ảnh hưởng của sóng, dầu và môi trường):
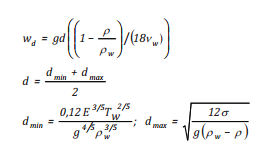 (20)
(20)
Vậy, quá trình xáo trộn dầu và di chuyển thẳng đứng phụ thuộc vào đặc điểm tính chất dầu (mật độ, độ nhớt) và ảnh hưởng môi trường (mật độ, độ nhớt, sóng, dòng chảy và gió) và thời gian. Từ các kết quả nghiên cứu trên, nhóm tác giả đưa ra hệ thống công thức liên quan đến tốc độ xáo trộn thẳng đứng [10]:
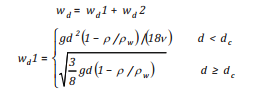 (21)
(21)
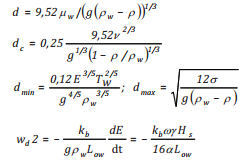 (21a)
(21a)
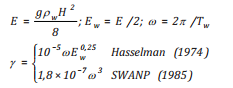 (21b)
(21b)
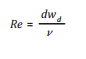 (21c)
(21c)
Trong đó:
N(d): Số lượng các giọt dầu trên một đơn vị thể tích nước;
V: Thể tích dầu trong tất cả các giọt dầu trong đơn vị thể tích lớp nước xáo trộn (m3);
Vd: Thể tích của giọt dầu (m3);
ε: Tốc độ tiêu tán năng lượng trung bình (J/s);
η= (v3/ ε)1/4: Quy mô độ dài micro Kolmogorov;
DS là theo Delvigne và Sweeney [20, 21]; HZ là theo Hinze [22]; LG là theo Li và Garrett [23]; trong đó, ow: Tốc độ xáo trộn giọt dầu (1/s);
Low : Tham số quy mô độ dài theo phương đứng (m), phụ thuộc vào kiểu sóng đổ;
α: Tham số phụ thuộc vào trạng thái mặt biển (1,2 -1,6);
kb: Hệ số (kb ~ 0,3 - 0,5) theo Lamarre và Melville [34];
g: Gia tốc trọng trường (m/s2);
Hs: Độ cao sóng (m);
Tw: Chu kỳ sóng (s);
E: Năng lượng sóng (J);
t: Thời gian (s);
C(0): Tham số phụ thuộc vào nhiệt độ và độ nhớt của dầu;
DBA: Tham số phụ thuộc vào độ cao sóng có nghĩa;
A: Diện tích dầu (m2);
∆d: Khoảng giới hạn đường kính giọt dầu là 1.130μm (các giọt dầu chủ yếu được tập trung trong khoảng từ 75- 320mm) với xu hướng nhẹ cho trung bình của phân bố kích thước giọt để thay đổi để kích thước nhỏ hơn với thời gian bất ổn ngày càng tăng;
wd: Vận tốc nổi của giọt dầu (m/s);
d: Đường kính giọt dầu (d = 100);
p và pw: Mật độ dầu và nước biển (kg/m3)
v và vw : Nhớt động học và dầu của nước (cSt)
μ và μw : Độ nhớt động lực dầu và nước (cP)
d: đường kính giọt dầu (d=100)
dmin và dmax: Đường kính của giọt dầu cực tiểu và cực
đại (mm);
σ: Sức căng bề mặt (N/m);
Re: Số Reynolds của giọt dầu.
2.4. Quá trình lan truyền dầu ngẫu nhiên (Random Walk)
Trong môi trường rối đồng nhất dừng, chuyển động hỗn loạn của chất lỏng và các hạt vật chất có thể xấp xỉ bằng quá trình di chuyển ngẫu nhiên trong mô hình. Đối với một chuỗi các bước thời gian, có thể giả thiết:
- Mỗi bước không tương quan với bước trước đó;
- Mỗi giọt dầu được mang bởi dòng chảy nền và bị dịch chuyển trong trường 3 chiều do tác động của các xoáy rối;
- Mỗi giọt dầu có tính chất riêng và dịch chuyển trong tương tác với các giọt dầu khác một cách ngẫu nhiên.
Theo mô hình ngẫu hành, khối lượng dầu có thể biểu diễn là tập hợp của N giọt dầu riêng biệt. Mỗi giọt dầu chuyển động theo 3 chiều với phương trình chuyển động của tấm quán tính của giọt thứ i có dạng.
Chuyển động rối u’, v’, w’ được tính theo phương pháp ngẫu nhiên theo Kitanidis [33] dưới dạng:
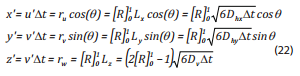 (22)
(22)
Trong đó:
∆t: Bước thời gian (s);
Dhx và Dhy: Hệ số rối ngang theo trục x và y (0 - 10m2/s);
Dz: Hệ số rối thẳng đứng (10-6 - 10-2m2/s);
Rn: Biến ngẫu nhiên có phân bố chuẩn [0,1];
ɵ: Biến ngẫu nhiên phân bố quanh phạm vi [0,2 ];
Lx, Ly và Lz: Bán kính khuếch tán theo trục x, y và giới hạn (m).
Góc lái một góc ɵ thống nhất phân phối ngẫu nhiên giữa 0 và 2π ;
p.e. ɵ = 2 π [ R]10
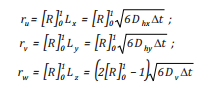 (22a)
(22a)
Trong đó 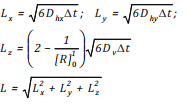 (22b)
(22b)
Từ phương trình (22) và dựa trên cơ sở tính chất tự nhiên của chất lỏng (chất lỏng tự cân bằng trên quá trình khuếch tán từ nơi có nồng độ cao hơn khuếch tán đến nơi có nồng độ thấp hơn), nhóm tác giả đưa ra hệ thống công thức liên quan đến quá trình khuếch tán di chuyển ngẫu nhiên [10]:
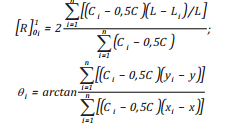 (23a)
(23a)
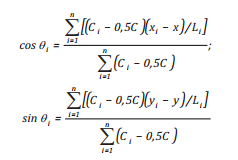 (23b)
(23b)
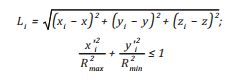 (23c)
(23c)
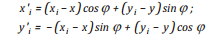 (23d)
(23d)
Trong đó:
L: Bán kính khuếch tán giới hạn (m);
Li: Khoảng cách từ điểm cần tính đến điểm thứ i nằm trong giới hạn của bán kính khuếch tán (m);
C và Ci: Nồng độ của điểm cần xác định và điểm thứ i (kg/m2);
x và xi: Vị trí theo trục x của điểm cần xác định và điểm thứ i (m);
y và yi: Vị trí theo trục y của điểm cần xác định và điểm thứ i (m);
n: Tổng số số điểm nằm trong giới hạn bán kính L;
x’i và y’i: Vị trí điểm theo hệ trục tọa độ của hướng gió trung trục x’;
φ: Hướng gió so với trục x.
3. Mô phỏng và đánh giá kết quả
Để mô phỏng các quá trình, nhóm tác giả giả định các thông tin cơ bản về dầu và môi trường xung quanh làm cơ sở cho việc mô phỏng các quá trình phong hóa dầu (Bảng 1).
Hình 1 - 12 thể hiện kết quả tính toán dựa trên công thức của nhóm tác giả và có so sánh với các công thức đã được công bố trong các công trình nghiên cứu khác.
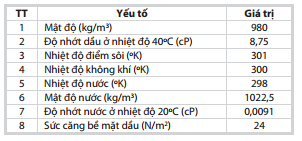 |
| Bảng 1. Đặc điểm dầu thô được sử dụng trong mô phỏng các quá trình phong hóa |
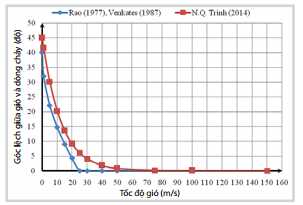 |
| Hình 1. Tương quan giữa tốc độ gió (Vw) và góc lệch ( ) hướng dòng chảy gió với hướng gió (Công thức 2a và 2b) |
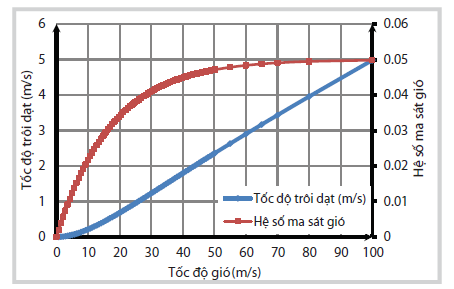 |
| Hình 2. Tương quan tốc độ (Vw) với hệ số ma sát ( w) và tốc độ trôi (αw x V w của gió (Công thức 1b và 2c) |
 |
| Hình 3. Tương quan tốc độ (Vc) với hệ số kéo ( c) và tốc độ trôi ( c x Vc) của dòng chảy (Công thức 1b và 3) |
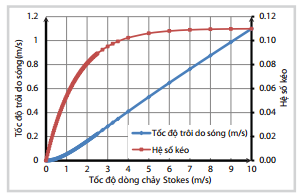 |
| Hình 4. Tương quan tốc độ (Vs) với hệ số trôi ( s) và tốc độ trôi ( s x Vs) của dòng chảy Stokes (công thức 1b và 4b) |
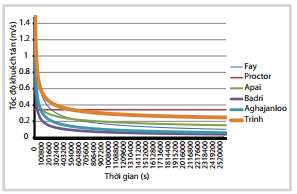 |
| Hình 5. Biến đổi tốc độ khuếch tán ngang theo thời gian |
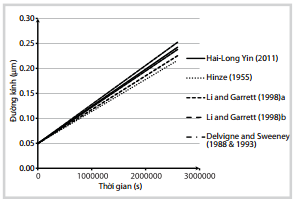 |
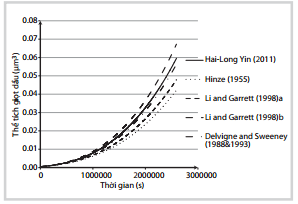
| Hình 6. Biến đổi đường kính giọt dầu theo thời gian |
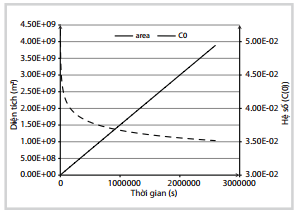 |
| Hình 7. Biến đổi diện tích loang và hệ số C(0) theo thời gian (công thức 13) |
 |
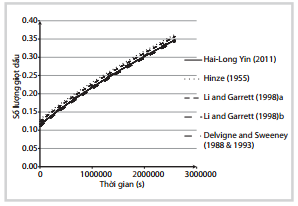
| Hình 8. Biến đổi thể tích giọt dầu theo thời gian |
 |
| Hình 9. Biến đổi số lượng dầu theo thời gian |
3.1. Quá trình bình lưu
Hình 1 - 4 là kết quả tính toán mô phỏng các hệ số tương quan, chuyển đổi từ các quá trình bình lưu của môi trường (gió, dòng chảy và sóng) tác động lên dầu tràn dựa trên công thức của nhóm tác giả, có so sánh với các công thức đã được công bố trong các nghiên cứu trước đó.
Đồ thị trên các hình vẽ mô phỏng cho thấy sự biến thiên thiên khá phù hợp dạng định tính với các giá trị có giới hạn.
3.2. Quá trình khuếch tán
Hình 5 thể hiện kết quả tính toán quá trình khuếch tán dầu dựa trên công thức của nhóm tác giả, có so sánh với các công thức đã được công bố trong các nghiên cứu trước đó. Đồ thị thể hiện sự tác động của nội lực do tính chất dầu tràn và ngoại lực do tác động của môi trường (như gió, dòng chảy và sóng).
3.3. Quá trình xáo trộn và di chuyển thẳng đứng
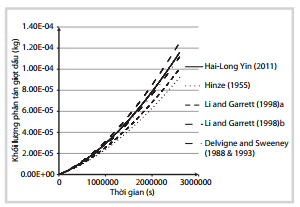 |
Hình 10. Biến đổi khối lượng phân tán giọt dầu theo thời gian
|
 |
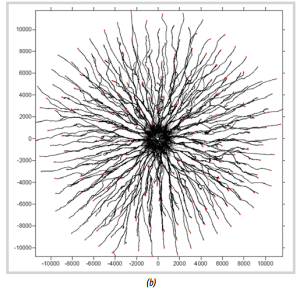 |
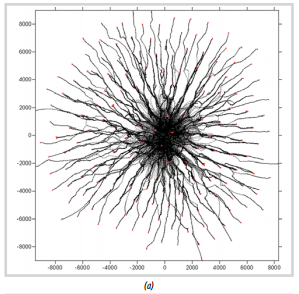
Hình 11. Kết quả mô phỏng quỹ đạo giọt dầu lan truyền ngẫu nhiên (Random Walk): sau 5 giờ (a); sau 10 giờ (b) |
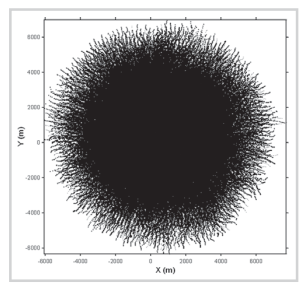 |
| Hình 12. Mô phỏng trường phân bố quỹ đạo giọt dầu sau 73 giờ tràn ra với nồng độ khác nhau tương ứng với đường kính hạt |
Hình 6 - 10 là kết quả tính toán mô phỏng các công thức từ 11 - 21 về quá trình xáo trộn và di chuyển thẳng đứng của các giọt dầu có sự biến đổi về đường kính, diện tích, thể tích và khối lượng phân tán dầu dựa trên các công thức mà nhóm tác giả tổng hợp từ các công trình nghiên cứu khác nhau. Kết quả cho thấy sự thay đổi của các công thức là khác nhau nhưng có chung quy luật biến đổi.
3.4. Quá trình lan truyền dầu ngẫu nhiên
Hình 11 và 12 là kết quả tính toán quá trình lan truyền dầu ngẫu nhiên dựa trên công thức của nhóm tác giả.Trong đó, tính chất dầu tràn có vai trò quyết định sự di chuyển của các giọt dầu. Quỹ đạo đường đi của các giọt dầu là ngẫu nhiên thể hiện độ tin cậy của công thức.
4. Kết luận
Kết quả tính toán mô phỏng cho thấy các quá trình vật lý quyết định khả năng di chuyển của dầu tràn. Mô hình hóa và tính toán các quá trình này cần xét đến các tham số phụ thuộc liên quan (thể hiện rõ trong phần mô phỏng tính toán quá trình bình lưu). Khả năng khuếch tán phụ thuộc vào tính chất dầu tràn và các tác động từ môi trường (như gió, dòng chảy và sóng). Quá trình xáo trộn thẳng đứng được nhóm tác giả xem xét trong nghiên cứu với mức độ thay đổi của các công thức khá đồng nhất về quy luật. Ngoài ra, quá trình lan truyền ngẫu nhiên cũng được xem xét và mô phỏng bằng các công thức của nhóm tác giả, từ đó xác định được bức tranh mô phỏng quỹ đạo di chuyển của các giọt dầu là ngẫu nhiên. Nhóm tác giả so sánh kỹ thuật giữa kết quả tính toán dựa trên các công thức đã được công bố trong các nghiên cứu trước đó và phương trình bán thực nghiệm của nhóm tác giả để đánh giá xác nhận mô hình toán học do thiếu dữ liệu đầu vào.
Mô hình mô phỏng các quá trình vật lý sẽ được áp dụng để tính khả năng di chuyển và biến đổi dầu thất thoát đồng bộ, phát triển sự ổn định của vết dầu loang trên mặt nước.
Tài liệu tham khảo
1. Rodney J.Sobey, Christopher H.Barker. Wave-driv- en transport of surface oil. Journal of Coastal Research. 1997; 13(2): p. 490 - 496.
2. American Society of Civil Engineers (ASCE). State- of-the-art review of modeling transport and fate of oil spills. ASCE, Journal of Hydraulic Engineering. 1996; 122(11): p. 594 - 609.
3. Mark Reed, Øistein Johansen, Per Johan Brand- vik, Per Daling, Alun Lewis, Robert Fiocco, Don Mackay, Richard Prentki. Oil spill modeling towards the close of the 20th century: Overview of the state of the art. Spill Science &
Technology Bulletine. 1999; 5(1): p. 3 - 16.
4. R.Periáñez. Chemical and oil spill rapid response modelling in the Strait of Gibraltar-Alborán Sea. Ecological Modelling. 2007; 207(2 - 4): p. 210 - 222.
5. K.D.Stolzenbach, O.S.Madsen, E.E.Adams, p. 271 - 282. A.M.Pollak, C.K.Cooper. Review and evaluation of basic techniques for predicting the behaviour of surface oil slicks. Massachusetts Institute Technology. 1977.
6. Ana J.Abascal, Sonia Castanedo, Fernando J.Mendez, Raul Medina, Inigo J.Losada. Calibration of a la- grangian transport model using drifting buoys deployed dur- ing the prestige oil spill. Journal of Coastal Research. 2009;
25(1): p. 80 - 90.
7. K.Shankar Rao. Source estimation methods for at- mospheric dispersion. Atmospheric Environment. 2007; 41(33): p. 6964 - 6973.
8. S.Venkatesh, T.S.Murty. Numerical simulations of the movement of the 1991 oil spills in the Arabian Gulf. Wa- ter, Air, and Soil Pollution. 1994; 74: p. 211 - 234.
9. Vagn Walfrid Ekman. On the influence of the earth’s rotation on ocean currents. Arkiv för Matematik, Astronomi och Fysik. 1905; 2(11): p. 1 - 52.
10. Nguyễn Quốc Trinh, Nguyễn Minh Huấn, Phùng Đăng Hiếu. Nghiên cứu lan truyền dầu ở Biển Đông phục vụ cảnh báo và tìm kiếm nguồn thải. Báo cáo tiến độ nghiên cứu sinh. Trường Đại học Khoa học Tự nhiên - Đại học Quốc gia Hà Nội. 6/2014.
11. Hugo B.Fischer, E.John List, Robert C.Y.Koh, Jorg Imberger, Norman H.Brooks. Mixing in inland and coastal
waters. Academic Press. 1979.
12. Akira Okubo. Oceanic diffusion diagrams. Deep- Sea Research and Oceanographic. 1971; 18(8): p. 789 - 802.
13. James A.Fay, David P. Hoult. Physical processes in the spread of oil on a water surface. International Oil Spill Conference Proceedings. 1971.
14. Roger Proctor, Roger A.Flather, Alan J.Elliot. Mod- elling tides and surface drift in the Arabian Gulf – Application to the Gulf oil spill. Continental Shelf Research. 1994; 14(5): p. 531 - 545.
15. O.Johansen. Particle in fluid model for simulation of oil drift and spread - Part I: Basic concepts. Oceanographic Center, Sintef Group, Norway. 1985.
16. M.A.Badri, A.R.Azimian. Oil spill model based on the Kelvin wave theory and artificial wind field for the Per- sian Gulf. Indian Journal of Marine Science. 2010; 39(2): p. 165 - 181.
17. Pavel Tkalich. A CFD solution of oil spill problems. Environmental Modelling and Software. 2006; 21(2):
18. Ehsan Sarhadi Zadeh, Kourosh Hejazi. Eulerian oil spills model using finite-volume method with moving boundary and wet-dry fronts. Modelling and Simulation in Engineering. 2012.
19. K.Aghajanloo, M.D.Pirooz, M.M.Namin. Numerical simulation of oil spill behavior in the Persian Gulf. International Journal of Environmental Research. 2013; 7(1): p. 81 - 96.
20. G.A.L.Delvigne, C.E.Sweeney. Natural dispersion of oil. Oil and Chemical Pollution. 1988; 4: p. 281 - 310.
21. G.A.L.Delvigne. Natural dispersion of oil by dif- ferent sources of turbulence. International Oil Spill Con- ference Proceedings. 1993. p. 415 - 419.
22. J.O.Hinze. Fundamentals of the hydrodynamics mechanisms of splitting in dispersion process. AIChE Jour- nal. 1955; 1(3): p. 289 - 295.
23. M.Li, C.Garrett. The relationship between oil drop- let size and upper ocean turbulence. Marine Pollution Bul- letin. 1998; 36: p. 961 - 970.
24. P.P.K.Raj. Theoretical study to determine the sea state limit for the survival of oil slicks on the ocean. United States Coast Guard. 1977.
25. W.D.Forrester. Distribution of suspended oil par- ticles following the grounding of the tanker Arrow. Journal of Marine Research. 1971; 29(2): p. 151 - 170.
26. M.L.Spaulding, E.Howlett, E.Anderson, K.Jayko. OILMAP: A global approach to spill modeling. 15th Arctic and Marine Oil Spill Program Technical Seminar, Canada. 1992; 25(4): p. 15 - 21.
27. K.Aravamudan, P.Raj, John Ostund, E.Newman, W.Tucker. Break up of oil on rough seas-simplified models and step-by-step calculation. United States Coast Guard. 1982.
28. S.S.Kutateladze, M.A.Styrikovich. Hydrodynamics of gas-liquid systems. Energy Publishers. 1976.
29. A.H.Al-Rabeh, H.M.Cekirge, N.Gunay. A stochas- tic simulation model of oil spill fate and transport. Applied Mathematical Modelling. 1989; 13(6): p. 322 - 329.
30. X.Chao, J.Shankar, H.F.Cheong. Two-and three- dimensional oil spill model for coastal waters. Ocean Engi- neering. 2001; 28(12): p. 1557 - 1573.
31. Deborah P.French-McCay. Oil spill impact model- ing: Development and validation. Environmental Toxicol- ogy and Chemistry. 2004; 23(10): p. 2441 - 2456.
32. Hai-Long Yin, Zu-Xin Xu, Chen Wang, and Da Yu. Development of early warning modeling system for sudden chemical spill in plain river network. Journal of Marine Sci- ence and Technology. 2011; 19(6): p. 634 - 642.
33. P.K.Kitanidis. Particle-tracking equations for the solution of the advection-dispersion equation with variable coefficients. Journal of Water Resources Research. 1994; 30(11): p. 3225 - 3227.
34. E.Lamarre, W.K.Melville. Air entrainment and dis- sipation in breaking waves. Nature. 1991; 351: p. 469 - 472.
Evaluation of oil spill physical processes in the marine environment
Nguyen Quoc Trinh1, Nguyen Minh Huan2
Phung Dang Hieu3, Nguyen Quang Vinh4
1. National Centre for Hydro-Meteorological Forecasting, MONRE
2. Ha Noi University of Science , VNU
3. Viet Nam Institute of Seas, MONRE
4. Aero Meteorological Observatory , MONRE
Summary
The article introduces some evaluation of oil spill physical processes in the marine environment under the discrete modelling method on the basis of considering the physical processes such as advection, diffusion, upright scrambling and random walk. Based on the most popular formula in the world and comparing results and analysis data, the authors have developed appropriate equations to simulate the physical processes, calculate the coefficients, and pa-
rameterise the physical processes affecting the oil spill and the random interaction process of spilled oil.
Key words: Oil spill, physical processes, mathematical simulation.