Tóm tắt
Các nghiên cứu phân tích sự cố xảy ra với dây neo của các bể chứa nổi FSO dạng CALM của Liên doanh Việt – Nga “Vietsovpetro” tại mỏ Bạch Hổ [1] cho thấy nhu cầu cấp bách cần phát triển các công trình biển (trong đó có FPSO) được thiết kế, lắp đặt và khai thác an toàn trong điều kiện khắc nghiệt của biển Việt Nam.
Một nghiên cứu tổng hợp đối với hệ thống neo công trình biển nổi đã được thực hiện bởi tác giả, dựa trên việc giải một loạt bài toán liên hoàn: lực thủy động học bậc 2, phản ứng động ngẫu nhiên, phân tích tổn thất mỏi ngẫu nhiên và đánh giá tuổi thọ mỏi của hệ dây neo. Một nghiên cứu tiếp theo của tác giả đã đưa ra quan điểm mới sát với điều kiện thực tế chịu tải của hệ dây neo để đánh giá độ tin cậy tổng thể hệ dây neo theo mô hình xác suất. Đó là độ tin cậy tổng hợp được xác định trong điều kiện biển cực đại có kể đến quá trình tích lũy tổn thất mỏi của dây neo. Cuối cùng, trong phần nghiên cứu ứng dụng, tác giả đã tính toán cho hệ dây neo bể chứa nổi FSO VSP-01 khai thác tại mỏ Bạch Hổ ở vùng biển Việt Nam.
Nghiên cứu này dựa trên bằng sáng chế đồng tác giả [2] và cuốn sách của tác giả đã được xuất bản tại Nhà xuất bản Presses Académiques Francophones (PAF) Cộng hòa Liên bang Đức [3].
Từ khóa: Độ tin cậy, lực thủy động học bậc 2, phản ứng động ngẫu nhiên, tổn thất mỏi ngẫu nhiên, tuổi thọ mỏi, hệ thống neo giữ, bể chứa nổi FPSO, FSO.
1. Giới thiệu
Xu hướng trên thế giới là dần thay thế các công trình biển cố định bằng các công trình nổi nói chung và bể chứa nổi FPSO nói riêng để khai thác dầu khí tại độ sâu nước ngày càng tăng do các công trình nổi có ưu thế hơn so với giàn cố định như: lợi ích kinh tế (không cần đường ống ngầm để vận chuyển dầu), linh hoạt trong sử dụng (từ vùng nước nông đến vùng nước sâu), có thể di chuyển từ mỏ này sang mỏ khác và khả năng chứa đựng dầu lớn. Công trình bể chứa nổi FPSO được neo giữ bởi hệ thống các dây neo mà đầu dây được cố định dưới đáy biển bằng các neo. Dạng neo một điểm neo (single point mooring - SPM) là dạng phổ biến nhất, trong đó loại Turret (Hình 1) có độ an toàn cao nhất. SPM cho phép bể chứa nổi có thể xoay quanh vị trí neo giữ để chịu tải trọng môi trường ít nhất.

Tổng hợp phân tích các nguyên nhân của các sự cố xảy ra với các công trình biển nổi có neo giữ nói chung và các bể chứa nổi và rót dầu FPSO nói riêng tại mỏ Bạch Hổ [1] cho thấy sự cố hường xảy ra tại các dây neo do điều kiện môi trường biển khắc nghiệt thường xuyên xảy ra bão nhiệt đới và gió mạnh kết hợp với tổn thất mỏi tích lũy trong dây neo. Do đó, việc xác định độ tin cậy tổng thể kết hợp giữa độ tin cậy bền và mỏi theo phương pháp xác suất của hệ thống neo của các công trình biển nổi là bài toán có ý nghĩa đặc biệt quan trọng để phản ánh được chính xác nhất phản ứng của kết cấu dưới tác dụng của các lực ngẫu nhiên của môi trường biển. Nghiên cứu tất cả các bài toán của dây neo để nghiên cứu độ tin cậy của hệ dây neo.
Sự phát triển các bể chứa nổi FPSO: FPSO (Floating Production Storage Offloading) là một công trình nổi để khai thác, xử lý, chứa đựng và rót dầu trên biển, có hình dạng giống một con tàu được trang bị các thiết bị cần thiết để khai thác và xử lý dầu, có các khoang chứa dầu thô được lấy từ các đầu giếng dầu dưới đáy biển thông qua các đường ống mềm (risers). FPSO được neo giữ tại vị trí khai thác bởi hệ thống dây neo (neo quanh một điểm hoặc nhiều điểm) và các neo cố định với đáy biển. Còn FSO (Floating Storage and Offloading) là một bể chứa nổi tương tự FPSO, nhưng không có chức năng xử lý dầu, không có các thiết bị phục vụ việc xử lý dầu, khí.
Từ năm 1977, các FPSO đã được sử dụng để phát triển các mỏ nhỏ, ở vùng nước nông, trong điều kiện môi trường không khắc nghiệt, không có hạ tầng các đường ống ngầm. Việc sử dụng FPSO cho phép giảm thiểu chi phí lắp đặt đường ống ngầm vận chuyển dầu. Từ năm 1986 FPSO đã được sử dụng ở biển Bắc, khởi đầu cho việc ứng dụng tại các vùng biển nước sâu.
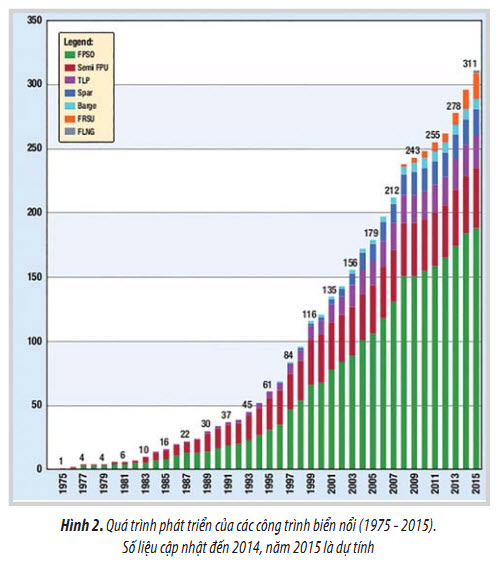
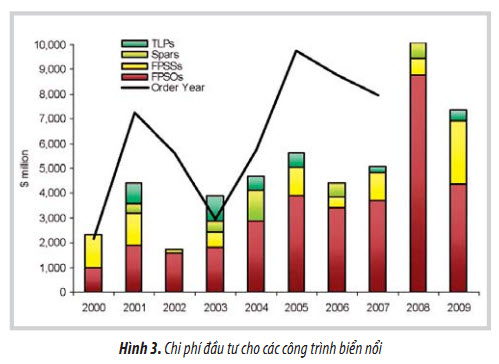
Theo số liệu thống kê tính đến tháng 5/2015 đã có 167 FPSO đang khai thác trên tổng số 273 công trình biển nổi trên thế giới. Số lượng FPSO hoán cải nhiều hơn đóng mới vì FPSO hoán cải từ tàu dầu có giá thành thấp hơn, thời gian hoàn thành nhanh hơn. Từ năm 1995 đến nay, số lượng FPSO có sự tăng trưởng nhanh. Trong 14 năm (1995 - 2008), 94 FPSO đã được lắp đặt, trung bình 6,7 FPSO/ năm. Trong số đó, 46 FPSO được đưa vào sử dụng trong 5 năm (1995 - 1999), trung bình 9 FPSO/năm. Đặc biệt từ 1996, với sự khám phá của các mỏ mới có độ sâu nước lớn, số lượng FPSO tăng vọt. Từ độ sâu trên 1.000m, có 22 FPSO đang khai thác. Độ sâu nước lớn nhất là Pioneer của BP (2012) 2.600m, trong dự án độ sâu lớn nhất là Turitella của Shell (2016) 2.896m (9.500ft). Số lượng các công trình biển nổi được đưa vào khai thác cũng như chi phí đầu tư tăng nhanh sau từng năm, đặc biệt là dạng FPSO chiếm 61,2% các công trình biển nổi (Hình 2 và 3).
Nội dung nghiên cứu đánh giá độ tin cậy tổng thể của hệ dây neo bể chứa nổi bao gồm các bài toán:
+ Lực thủy động bậc 2 tần số thấp lên kết cấu bể chứa nổi: tính lực sóng, chuyển vị;
+ Phân tích động ngẫu nhiên cho hệ dây neo => bài toán kiểm tra bền (ULS);
+ Phân tích mỏi ngẫu nhiên cho hệ dây neo => kiểm tra mỏi (FLS), tính tuổi thọ mỏi;
+ Độ tin cậy tổng hợp dựa trên phương pháp xác suất: đóng góp mới.
Các bài toán trên được thực hiện theo thuật toán tính toán hệ dây neo bể chứa nổi ở mục 5 (Hình 6).
2. Xác định lực thủy động ngẫu nhiên tác động lên bể chứa nổi FPSO [4 - 6]
Phần này trình bày khái quát về tải trọng động ngẫu nhiên của sóng (lực thủy động) tác động lên kết cấu nổi có dây neo. Kết cấu nổi dạng tàu FPSO được coi là một vật thể kích thước lớn làm thay đổi nhiều đến chuyển động của sóng tới. Việc tính toán các lực thủy động tác dụng lên kết cấu trong trường hợp này là giải bài toán nhiễu xạ - bức xạ bậc nhất và bậc hai.
2.1. Bài toán nhiễu xạ - bức xạ của sóng tác động lên kết cấu nổi
Khai triển chuỗi Taylor cho hàm thế vận tốc
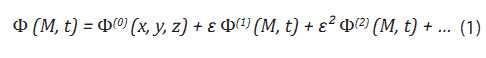
Với kết cấu nổi không có vận tốc:
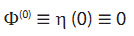
Bài toán nhiễu xạ - bức xạ bậc 1:
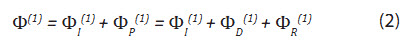
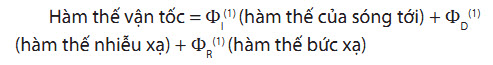
Bài toán nhiễu xạ - bức xạ bậc 2:
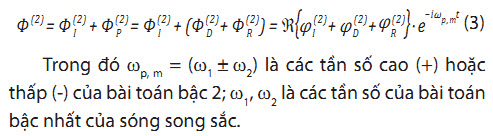
Hiện nay, nhiều mô hình số để giải bài toán nhiễu xạ - bức xạ đã được nghiên cứu và đưa vào sử dụng. Kết quả của các phần mềm tính này là hàm truyền (RAO – Response Amplitude Operator) của các thông số phục vụ cho tính toán thiết kế các công trình biển như: lực sóng bậc 1 và bậc 2, chuyển vị của kết cấu, áp lực lên kết cấu nổi, khối lượng nước kèm… Phần tính toán áp dụng số trong bài báo sử dụng phần mềm tính toán HydroStar For Expert của hãng Đăng kiểm Pháp Bureau Veritas.
2.2. Lực thủy động của sóng tác động lên kết cấu nổi
Ta có thể biểu diễn lực thủy động dưới dạng ma trận như sau:
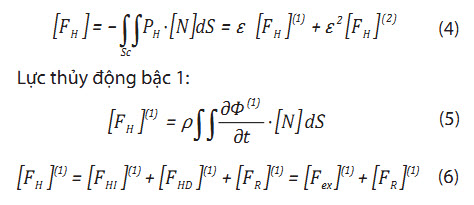
Từ (5) và (6), ta có công thức tính lực thủy động bậc 1 như sau :
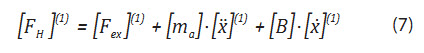
Lực thủy động bậc 2, với dạng tần số thấp (w1 - w2) là chuyển động dịch chuyển ngang của các kết cấu nổi có neo (lực trôi dạt chậm của FPSO) trong đó chu kỳ dao động riêng của nó tính bằng phút

Lực bậc 2 của sóng tần số thấp được xem là nguyên nhân chủ yếu gây cộng hưởng của kết cấu nổi có dây neo dạng FPSO do tác động của lực trôi dạt chậm.
Lực bậc 2 tần số thấp đối với sóng ngẫu nhiên được biểu diễn như sau:
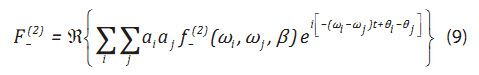
Với f−(2) (wi, wj, b) là hàm truyền bậc 2 (QTF – Quadratic Transfer Function) của lực sóng bậc 2 tần số thấp.
Lực trôi dạt chậm tác dụng lên kết cấu FPSO: Việc tính toán lực trôi dạt có ý nghĩa quan trọng trong việc thiết kế công trình để đảm bảo độ an toàn khi khai thác. Có 3 lý thuyết tính toán lực trôi dạt: Lý thuyết trường gần của Pinkster, lý thuyết trường xa của Maruo-Newman và lý thuyết trường trung gian của X.B.Chen [4]. Trong đó, lý thuyết trường trung gian là ưu việt nhất, được xây dựng trong một bề mặt nước xung quanh vật thể nổi, cách một khoảng xác định từ vật thể và khắc phục được nhược điểm của lý thuyết trường gần và lý thuyết trường xa.
Lực trôi dạt chậm tác dụng lên kết cấu FPSO: Việc tính toán lực trôi dạt có ý nghĩa quan trọng trong việc thiết kế công trình để đảm bảo độ an toàn khi khai thác. Có 3 lý thuyết tính toán lực trôi dạt: Lý thuyết trường gần của Pinkster, lý thuyết trường xa của Maruo-Newman và lý thuyết trường trung gian của X.B.Chen [4]. Trong đó, lý thuyết trường trung gian là ưu việt nhất, được xây dựng trong một bề mặt nước xung quanh vật thể nổi, cách một khoảng xác định từ vật thể và khắc phục được nhược điểm của lý thuyết trường gần và lý thuyết trường xa.
3. Phương pháp luận để kiểm tra bền hệ thống neo của công trình nổi [7, 8]
Phần này tác giả trình bày tóm tắt phương pháp luận phân tích và kiểm tra bền hệ thống neo của công trình nổi bằng cách sử dụng các mô phỏng tựa động và mô phỏng động ngẫu nhiên phi tuyến của dây neo theo phương pháp phân tích trong miền thời gian sử dụng kỹ thuật mô phỏng Monte-Carlo. Bài toán động ngẫu nhiên được thiết lập bởi các phương trình cơ bản của chuyển động của công trình nổi dưới tác dụng của các lực ngẫu nhiên. Phần tính toán ứng dụng của phần này sử dụng phần mềm ARIANE-3Dynamic của Đăng kiểm Pháp (Bureau Veritas).
3.1. Phương trình chuyển động của công trình nổi
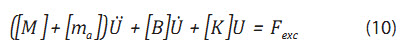
Trong đó:
[M]: Ma trận khối lượng (ma trận quán tính);
[ma]: Ma trận khối lượng nước kèm;
[B]: Ma trận cản;
[K]: Ma trận độ cứng của hệ, được xác định từ các đặc trưng thủy tĩnh của vật thể (KS), độ cứng phụ thêm của hệ neo (KA ) và của nước dằn (Kb);
U, U&, U&&: Véc tơ chuyển động, vận tốc và gia tốc chuyển động của bể chứa nổi;
Fexc: Các lực tác động cưỡng bức đến từ sóng tới và sóng nhiễu xạ.
3.2. Phản ứng của công trình nổi dưới tác dụng của sóng ngẫu nhiên
Phản ứng X của kết cấu (RAO) dưới tác dụng của song ngẫu nhiên là tổng của tất cả các phản ứng thành phần, do các sóng thành phần cấu thành ra sóng ngẫu nhiên đó tạo nên.
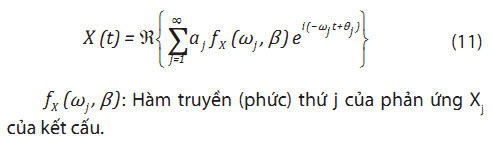
3.2.1. Phương pháp tựa động phân tích phản ứng ngẫu nhiên của dây neo [6, 8]
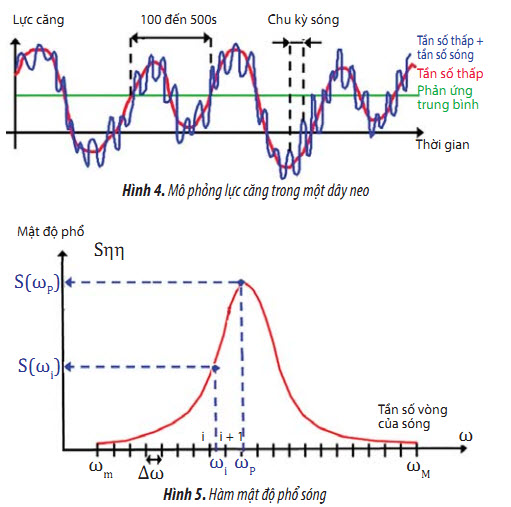
Bài toán được giải trong miền thời gian do cần giải quyết bài toán phi tuyến dây neo. Phương pháp tựa động thích hợp cho neo giữ trong vùng có độ sâu nước nông và vừa. Đầu tiên khi chưa có ngoại lực tác dụng, công trình nổi thiết lập vị trí cân bằng ban đầu do sức căng ban đầu của dây neo. Sau đó dưới tác động của lực trung bình của sóng, gió, dòng chảy, công trình nổi sẽ dịch chuyển tới một vị trí cân bằng trung bình mới. Tại đây, ngoại lực được cân bằng bởi sức căng của các dây neo tại đầu dây. Quanh vị trí cân bằng mới này, công trình nổi sẽ thực hiện các chuyển động tần số thấp và tần số sóng. Lúc này, các lựcquán tính được cân bằng với ngoại lực và lực căng của hệ dây. Ngoại lực tác dụng lên công trình nổi được neo giữ được phân thành các loại: lực trung bình, lực biến thiên chậm tần số thấp (Low Frequency), lực dao động tần số sóng (Wave Frequency), dẫn đến phản ứng đầu ra (lực căng) là mô phỏng gồm có 3 thành phần:
- Phản ứng trung bình: Cân bằng tĩnh bởi lực trung bình;
- Phản ứng tần số thấp: Áp dụng các lực tần số thấp tại vị trí cân bằng;
- Phản ứng tần số sóng: Thành phần thêm vào phản ứng tần số thấp (Hình 4)
a. Các bước mô phỏng tựa động trong miền thời gian:
- Giai đoạn phân tích tĩnh: Các tải trọng trung bình tác dụng lên công trình đưa công trình đến một vị trí cân bằng tĩnh.
- Giai đoạn phân tích tựa động: Bài toán lặp theo thời gian.
+ Phản ứng tần số thấp: Tính động của phần công trình nổi (tức là tính tựa động của dây vì chỉ xét cho điểm đầu dây), tại mỗi thời điểm t trong cơn bão, dưới tác dụng của lực tần số thấp (lực bậc 2 QTF), giải phương trình (10) cho ra dịch chuyển tần số thấp δLF.
+ Phản ứng tần số sóng (hiệu ứng bậc nhất): Thêm vào dịch chuyển bậc nhất gây ra bởi sóng (thông tin trong RAO): δWF. Dịch chuyển tổng cộng sẽ là: δtot = δLF + Δwf
- Xác định được lực căng tương ứng tại điểm đầu dây (fairlead) ở thời điểm t. Lặp lại vòng lặp cho đến khi t = 3 giờ, ghi lại được mô phỏng lực căng dây theo thời gian
b. Các quy ước tính toán trong miền thời gian theo phương pháp Monte Carlo:
• Giả định: Các hiện tượng tần số thấp và tần số song xảy ra độc lập với nhau
• Tín hiệu sóng: Phương pháp Monte Carlo cho phép biểu diễn một tập hợp sóng ngẫu nhiên (mật độ phổ sóng) bởi N (100 - 5.000) con sóng đơn Airy (Hình 5):
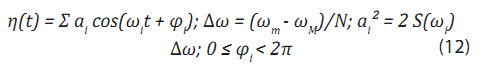
Trong đó:
η(t): Mặt đường nước tại thời điểm t;
ai ωi φi: Các thông số của sóng Airy thứ i;
S(ωi): Mật độ phổ của tần số wi.
• Các thông số tính toán: Một mô phỏng tựa động kéo dài 3 giờ; một bước thời gian thường lấy 1 giây; thời điểm bắt đầu ghi lại mô phỏng: sau khi 1 dây bị đứt hoặc khi hệ đã cân bằng.
c. Xác định lực căng thiết kế của dây neo theo miền thời gian
Đối với mỗi trạng thái biển tính toán phải thực hiện n lần mô phỏng, mỗi lần trong 3 giờ. Các mô phỏng lực căng của dây neo được xây dựng theo mỗi bước thời gian. Mỗi mô phỏng 3 giờ cho 1 giá trị lực căng lớn nhất, từ đó tính được giá trị trung bình và độ lệch chuẩn của n lực căng lớn nhất đó và tính được lực căng thiết kế của dây như sau:
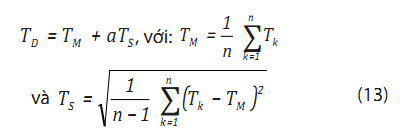
Trong đó:
TD: Lực căng thiết kế của dây;
n: Số lần mô phỏng;
Tk: Trị lực căng lớn nhất ở đầu dây đạt được trong mô phỏng thứ k;
TM: Giá trị trung bình của Tk sau n mô phỏng;
TS: Độ lệch chuẩn của (n-1) mô phỏng;
a: Hệ số phụ thuộc vào n và phương pháp phân tích [9, 10].
3.2.2. Động lực học của dây neo - Phân tích đầy đủ trong miền thời gian
Phương pháp này được áp dụng cho việc neo giữ ở vùng nước sâu hoặc điều kiện thời tiết rất khắc nghiệt và dùng cho phân tích mỏi. Trong phần nghiên cứu ứng dụng sau đây sử dụng module chương trình MCS Cable 3D. Bước thời gian tính động (Cable-3D) theo kinh nghiệm là 0,02 giây là cần thiết để đạt được một tín hiệu đầu ra tốt của lực căng động của dây neo, thậm chí nó còn cần phải giảm thêm nữa đối với trường hợp rất đặc biệt.
Hệ số an toàn trong tính bền của dây neo
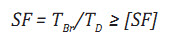 (14)
(14)
Trong đó: TBr là lực đứt tới hạn của dây được cho trong số liệu đầu vào; [SF] là hệ số an toàn nhỏ nhất theo quy phạm [9]. Với phương pháp tựa động [SF] = 1,75, phương pháp động: 1,67
4. Phương pháp luận kiểm tra mỏi hệ thống dây neo FPSO
Trong số các lực tác dụng lên hệ FPSO neo giữ, có các lực gây ra bởi các trạng thái biển ngắn hạn với gió và dòng chảy kèm theo. Dưới đây là tóm tắt một số kết quả nghiên cứu mỏi trong miền thời gian cho hệ thống dây neo FPSO.
Có nhiều phương pháp để đếm chu trình của lực căng theo thời gian. Các phương pháp này có mục đích để phân tích mỏi của kết cấu công trình biển nói chung theo quy tắc Palmgren-Miner dựa trên phân tích trong miền thời gian để ước tính tuổi thọ của công trình. Phương pháp đếm giọt mưa hiện nay vẫn được dùng phổ biến nhất [11].
4.1. Đường cong mỏi T-N trong tính mỏi cho dây neo
Để đánh giá độ bền do mỏi của một dây neo trong hệ neo FPSO, cần xác định tuổi thọ của dây từ mô phỏng ngẫu nhiên sức căng của dây và từ đường cong mỏi T-N của dây đang xét thay vì đường cong S-N như đối với công trình giàn khoan cố định, với việc áp dụng luật Palmgren- Miner.
Đường cong mỏi T-N cho số chu trình trước khi xảy ra phá hủy của một dây neo [12].
Phương trình của đường cong mỏi T-N được viết dưới dạng sau:
NRm = K (15)
và dạng phương trình tuyến tính:
log10 N = log10 K - mlog10 R (16)
Trong đó:
N là số chu trình xảy ra phá hủy mỏi;
R = T V /TR: Tỷ số của sự biến đổi của lực căng (T V = Tmax - Tmin) so với độ bền phá hủy tối thiểu của dây cáp hoặc xích neo (kí hiệu là TR);
m và K: Các hệ số đưa ra bởi tiêu chuẩn thiết kế API RP2SK [12].
4.2. Tuổi thọ mỏi của một dây neo
Dùng luật Palmgren-Miner để xác định tổn thất mỏi trung bình trong 1 năm của dây neo:
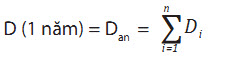 (17)
(17)
Trong đó:
n: Số lượng trung bình các trạng thái biển trong 1 năm;
Di: Hệ số tổn thất mỏi trung bình trong 1 năm của một dây neo được xét chịu tác dụng của các tải trọng môi trường ở trạng thái biển i (TTB i):
Di = Dwi + DLi (18)
Tổn thất mỏi trung bình trong 1 năm của dây neo trong miền thời gian:
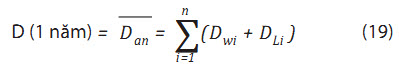
Hệ số tổn thất mỏi trung bình gây ra hoặc bởi lực sóng, hoặc bởi lực trôi dạt tần số thấp trong TTB i (kí hiệu Dwi và DLi).
Tuổi thọ trung bình do mỏi của một dây neo:
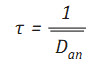 (20)
(20)
Theo [12], hệ số an toàn cho phép trong tính mỏi là 3, hay tuổi thọ mỏi tính toán ít nhất phải bằng 3 lần tuổi thọ mỏi tối thiểu dự kiến trong thiết kế.
5. Phương pháp đánh giá độ tin cậy tổng thể của hệ thống dây neo FPSO [3, 6, 13]
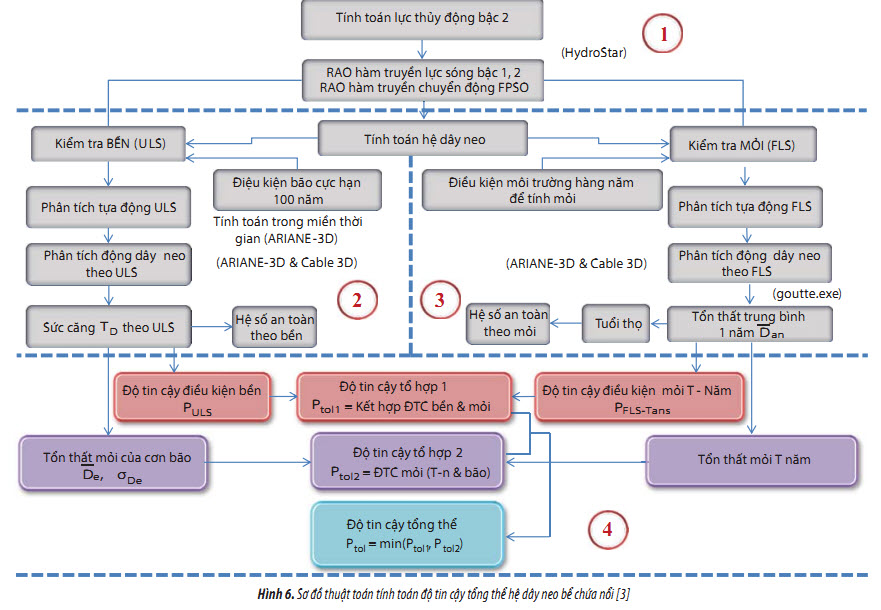
Hình 6 thể hiện thuật toán để giải quyết 4 bài toán như sau:
(1) Tính toán lực thủy động của sóng tác động lên công trình nổi bằng phần mềm HydroStar.
- Kết quả cho ra hàm truyền RAO của phản ứng của kết cấu.
- Từ đó tiến hành tính toán hệ dây neo theo 2 trạng thái giới hạn bền và mỏi.
(2) Bài toán tính toán hệ dây neo theo điều kiện bền (ULS) gồm có 2 bài toán:
- Phân tích tựa động dây neo trong miền thời gian, sử dụng chương trình ARIANE-3D
- Phân tích động đầy đủ cho dây neo trong miền thời gian, sử dụng chương trình ARIANE-3D kết hợp với module MCS Cable 3D.
(3) Bài toán phân tích mỏi ngẫu nhiên (FLS): phần 1 tương tự bài toán bền nhưng với số liệu môi trường để tính mỏi, phần 2 từ kết quả lực căng dây trong miền thời gian để tính tổn thất mỏi tích lũy bằng chương trình Goutte.exe.
(4) Tính toán độ tin cậy tổng thể cho hệ dây neo từ kết quả của bài toán 3 và 4.
- Tổ hợp 1: Tổ hợp độ tin cậy bền và độ tin cậy mỏi tích lũy trong T năm: Ptot1 (ULS, FLS-Tnăm)
- Tổ hợp 2: Tính độ tin cậy mỏi (FLS) là tổ hợp của tổn thất mỏi tích lũy trong T năm khai thác (FLS-Tnăm) và tổn thất mỏi tích lũy trong trạng thái biển cực hạn (bão 100 năm), từ đó tính độ tin cậy mỏi cho dây theo tổ hợp 2.
- Độ tin cậy tổng thể là giá trị nhỏ nhất của 2 tổ hợp trên.
Sơ đồ thuật toán của bài toán (4) đã được thiết lập và đánh giá trong [3] và [6]
5.1. Phương pháp truyền thống để đánh giá độ an toàn của dây neo
- Đánh giá độ an toàn của dây neo theo điều kiện bền (ULS)

Khi đó, sự chịu đựng của dây không đổi theo thời gian (t) (Hình 8a).
- Đánh giá độ an toàn của dây neo theo điều kiện mỏi (FLS)
Tổn thất mỏi tích lũy, ký hiệu là D (ti, năm), ta có:
D (to) = 0 < D (t1) < D (t2) < D (ti) < D(ti)max ≤ 1 (22)
Theo thời gian có sự xuống cấp của kết cấu, dẫn tới sự chịu đựng của dây giảm theo thời gian. Vì thế, tổn thất mỏi tích lũy tăng theo (t) (Hình 8b).
- Nhược điểm của phương pháp truyền thống: (i) ULS tại thời điểm ti (bão 100 năm), không kể đến sự xuống cấp của kết cấu do tổn thất mỏi tích lũy trong quá khứ [D(ti)]. Thực tế, sự chịu đựng thực của dây giảm theo thời gian; (ii) FLS tại thời điểm ti (tổn thất mỏi tích lũy), không kể đến sự xuất hiện của trạng thái biển cực hạn (3 - 6 giờ) tại thời điểm ti này. Do đó, tổn thất mỏi tích lũy D(i) (ti năm trạng thái biển bình thường) < D(i) (ti năm điều kiện biển bình thường + bão 100 năm) (do số chu trình của sức căng dây tăng).
5.2. Phương pháp xác suất đánh giá độ tin cậy tổng thể của dây neo
Phương pháp này là đóng góp mới của tác giả nhằm khắc phục các nhược điểm của phương pháp truyền thống.
5.2.1. Độ tin cậy của dây neo dựa theo phương pháp xác suất [2, 3]
Các trạng thái giới hạn (ULS và FLS) cho dây neo FPSO được xác định với cách tiếp cận mới, kết hợp trạng thái giới hạn ULS và FLS theo nguyên tắc xác suất, giúp cho ước tính chính xác hơn các ứng xử thực tế của hệ thống neo giữ FPSO.
- Độ tin cậy bền của dây neo (ULS) được xác định bởi biểu thức sau:
+ Độ tin cậy trong điều kiện bền của dây neo trường hợp phổ dải hẹp:
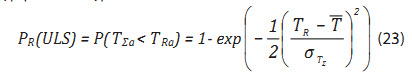
Trong đó: TRa là chênh lệch giữa lực kéo đứt tối thiểu (TR) và lực căng trung bình của dây ( T ): TRa = TR - T (24)
+ Độ tin cậy trong điều kiện bền của dây neo trường hợp phổ dải rộng:
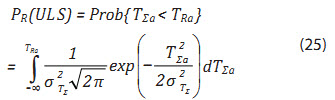
Phương trình (25) có thể viết dưới dạng thông số b theo [14]:
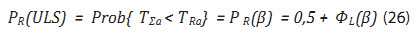
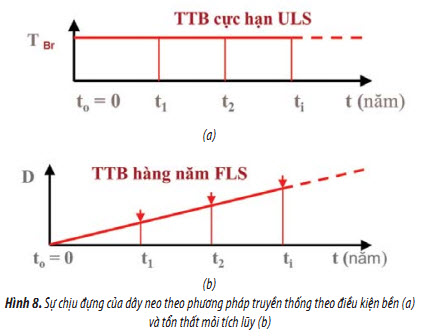
Trong đó: FL(x) là hàm Laplace, b là chỉ số độ tin cậy về bền của dây neo đang xét:
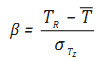 (27)
(27)
- Độ tin cậy mỏi của dây neo sau T năm khai thác PFat(FLS- Tnăm) được thiết lập tương tự:
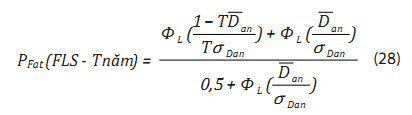
- Độ tin cậy tổng thể dựa trên nguyên tắc giao giữa hai sự kiện (A và B) [5]:
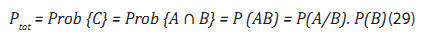
Giả thiết hai sự kiện độ tin cậy bền và mỏi (ULS và FLS) là độc lập => P(A/B) = P(A)
Độ tin cậy tổng thể theo [2]:

5.2.2. Phân tích ý nghĩa của việc xác định độ tin cậy tổng thể
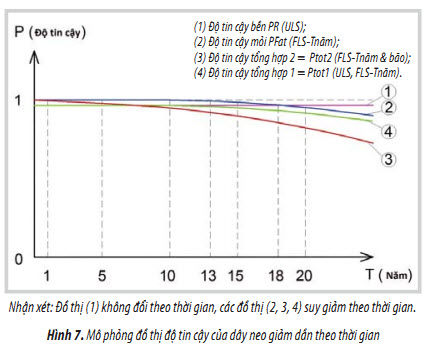
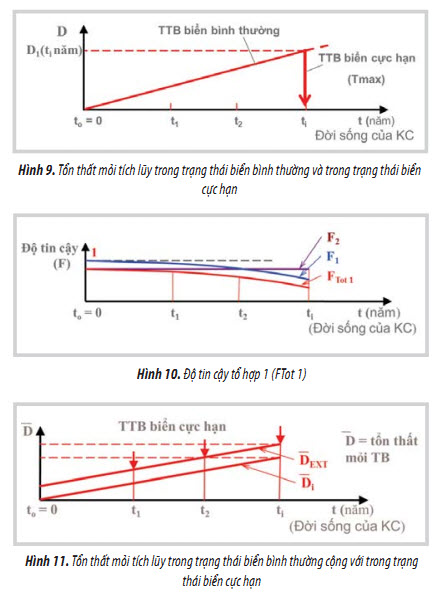
1 - Tích lũy tổn thất mỏi D tăng dần theo thời gian, xem Hình 9. Tại thời điểm ti, trong trạng thái biển bình thường FLS có tích lũy tổn thất mỏi D1 sau ti năm:
Độ tin cậy mỏi (giảm dần theo thời gian, xem Hình 10):
F1 = PF (FLS-tinăm) (33)
2 - Tại thời điểm ti, có trạng thái biển cực hạn có độ tin cậy trong điều kiện bền:
Độ tin cậy bền ULS (không đổi <1, xem Hình 10):
F2 = PR (ULS) = PR (Tmax < R) (34)
(1) Tổ hợp 1:
Độ tin cậy tổ hợp 1 FTot 1= Độ tin cậy bền (ULS) F2 có kể đến tổn thất mỏi tích lũy (FLS) F1:
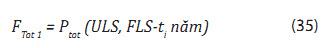
(được tính theo phương trình (31).
(2) Tổ hợp 2:
- Tổn thất mỏi tổng cộng tích lũy trong trạng thái biển cực hạn [DExt] và trong ti năm quá khứ [D1(ti năm)]:
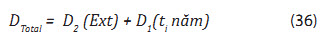
- Tổ hợp 2: Độ tin cậy tổ hợp 2 FTot 2 = Độ tin cậy xác định bởi tổn thất mỏi tổng cộng: tích lũy trong ti năm (D1) và tích lũy trong trạng thái biển cực hạn (D2), được tính theo phương trình (32)
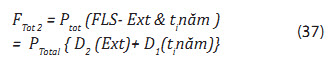
(3) Đánh giá an toàn của dây neo dựa trên độ tin cậy của kết cấu dây neo:
Độ tin cậy tổng thể của kết cấu:
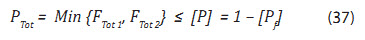
6. Áp dụng tính độ tin cậy tổng thể cho hệ thống dây neo FSO ở vùng biển Việt Nam [6]
Kết quả tính và so sánh độ tin cậy bền, mỏi và 2 tổ hợp độ tin cậy của dây neo FSO.
Sử dụng phần mềm: HydroStar, ARIANE-3D& Cable- 3D, SAP2000, Goutte để tính dây neo FSO VSP-01 ở mỏ Bạch Hổ [15] (dạng neo Turret Hình 13) 47m nước.
6.1. Kết quả tính toán lực và chuyển động của FSO sử dụng chương trình HydroStar
Các kết quả tính gồm: Hàm truyền RAO lực bậc nhất tác động lên FSO; RAO lực trôi dạt bậc 2 tác động lên FSO tính bởi 3 phương pháp: trường xa, trường gần, trường trung gian; hàm truyền bậc 2 (QTF) của lực sóng dùng trong tính dây neo; áp lực của sóng lên tàu FSO tại các điểm xác định trên vỏ tàu;
Tính toán chuyển động của FSO: Các kết quả đã tính toán gồm: Hàm truyền 6 chuyển động (3 dọc trục x, y, z; 3 quay quanh trục x, y, z) cho FSO dạng Turret, tại độ sâu nước d = 47m.
6.2. Kết quả tính toán phản ứng động của dây neo cho FSO sử dụng phần mềm ARIANE-3D So sánh các mô phỏng lực căng trong dây 3 giữa cách tính tựa động và tính động:
Hệ số an toàn của lực căng động của hệ dây neo nhỏnhất là ở dây 3 (điều kiện đầy tải): SF = 2,007 > 1,67 => tất cả hệ dây neo FSO dạng Turret đều thỏa mãn điều kiện bền trong cả 2 trường hợp tải trọng.
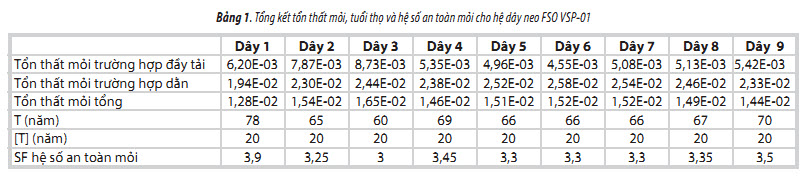
6.3. Kết quả tính tổn thất mỏi và tuổi thọ mỏi cho hệ thống dây neo FSO
Kết quả tính tổn thất mỏi và tuổi thọ mỏi cho hệ dây neo FSO VSP-01 (Bảng 1) cho thấy các hệ số an toàn về mỏi của tất cả các dây neo của FSO đều lớn hơn hoặc bằng 3, thỏa mãn với hệ số an toàn tới hạn qui định trong qui phạm [9, 10, 12]. Từ đó có thể kết luận rằng đối với bể chứa nổi FSO này, các lực căng thiết kế của hệ dây neo thỏa mãn điều kiện mỏi của lực căng cho phép trong dây neo đối với các trạng thái biển hàng năm của môi trường (FLS).

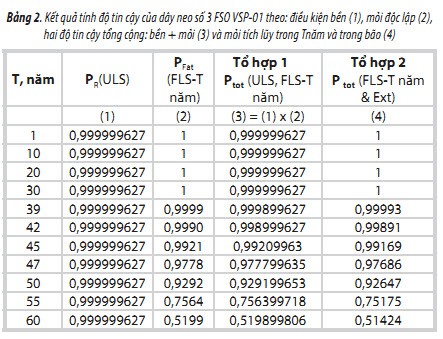
6.4. Kết quả tính độ tin cậy của dây neo FSO VSP-01
Kết quả tính độ tin cậy của dây neo số 3 FSO VSP-01 (Bảng 2) cho thấy độ tin cậy tổng cộng ở cả 2 tổ hợp 1 và tổ hợp 2 (cột 3 và 4) từ năm thứ 42 trở đi nhỏ hơn độ tin cậy bền hoặc mỏi tính riêng (cột 1, 2) và độ tin cậy tính theo tổ hợp 2 nhỏ hơn tổ hợp 1.
7. Kết luận
- Hệ dây neo FSO Turret đảm bảo cả điều kiện bền và mỏi dưới tác động của sóng ngẫu nhiên, trong cả 2 điều kiện dằn nước và đầy tải.
- Đề xuất phương pháp chọn cửa sổ thời gian cho mô phỏng động (quanh giá trị Tqsmax) do đó giảm thiểu thời gian tính động cho cả đánh giá bền và mỏi [6, 8].
- Đánh giá bền và mỏi cho dây neo theo các thành phần lực tần số thấp và lực tần số sóng cho thấy được bản chất của phản ứng của công trình biển neo giữ (lực trôi dạt bậc 2 quan trọng).
- Mô hình xác suất (tính cho miền thời gian) cho phép đánh giá sát thực phản ứng động ngẫu nhiên của dạng công trình này, từ đó đánh giá được độ tin cậy đồng thời của tổ hợp bền + mỏi (quan điểm mới áp dụng cho các công trình biển nổi).
Công hiến mới của tác giả nhằm xây dựng quy phạm mới về đánh giá sự an toàn của kết cấu:
- Phạm vi ứng dụng đối với tất cả các kết cấu công trình biển nói chung, đặc biệt cho vùng nước sâu hoặc/và trong điều kiện biển khắc nghiệt;
- Xu hướng: Đánh giá an toàn của kết cấu dựa trên phương pháp xác suất và độ tin cậy đang được phát triển, đóng góp mới của tác giả nhằm đề xuất cải tiến các quy phạm thiết kế công trình biển hiện hành.
Lời cám ơn
Bài báo dựa trên Đề tài nghiên cứu khoa học cấp Nhà nước [16], luận án Tiến sĩ [6] và sách [3] của tác giả. Xin chân thành cảm ơn Trường Đại học Xấy dựng, Bộ Giáo Dục và Đào tạo, Cơ quan Đăng kiểm Pháp và Nhà xuất bản PAF đã tạo cơ hội thuận tiện cho tác giả có điều kiện đạt được các kết quả nghiên cứu này.
Tài liệu tham khảo
1. Phạm Khắc Hùng. Đánh giá tổn thất của hệ neo FPSO ở mỏ Bạch Hổ, Việt Nam. Kết quả đề tài NCKH cấp Nhà nước. Báo cáo Số 3. 3/2004.
2. Phạm Khắc Hùng, Phạm Hiền Hậu. Phương pháp đánh giá an toàn cho các kết cấu công trình biển theo các điều kiện bền và mỏi mở rộng. Bằng Độc quyền sáng chế Số 10143. 2012.
3. Hien Hau Pham. FPSO - Fiabilité des lignes d’ancrage avec prise en compte de fatigue. ISBN- 13:978-3-8381-7928-5. Presses Académiques Francophones. 2015: 336p.
4. X.B.Chen (Bureau Veritas). Hydrodynamics in offshore and naval applications - Part I. Paper presented at the 6th Int. Conference on Hydrodynamics. Perth, Australia. 2004.
5. Molin Bernard. Hydrodynamique des Structures Offshore, Guides pratiques sur les ouvrages en mer. Editions Technip, Paris, France. 2002: 415p.
6. Phạm Hiền Hậu. Estimation de la fiabilité du système d’ancrage des FSO/FPSOs au Vietnam, avec prise en compte de l’accumulation du dommage de fatigue. PhD Thesis, University of Liège, Belgium. 4/2010.
7. Franck Legerstee (Bureau Veritas). Mooring Course. Shanghai. 2001: 55p.
8. Phạm Hiền Hậu. Phân tích tựa động và động ngẫu nhiên của hệ thống dây neo trạm chứa và rót dầu nổi (FPSO) trong điều kiện mỏ Bạch Hổ dựa trên các phần mềm Hydrostar và Ariane-3D. Tạp chí Dầu khí. 2009; 9: trang 35 - 42.
9. Bureau Veritas (Bureau Veritas). Quasi-Dynamic analysis of mooring systems using ARIANE software. Guidance Note NI 461 DTO R00 E, Bureau Veritas, Paris. 1998.
10. Bureau Veritas. Classification of mooring systems for permanent offshore units. Guidance Note NI 493 DTM R00 E, Paris. 2004.
11. ASTM. Standard practices for cycle counting in fatigue analysis. E 1049-85, ASMT International. 2005.
12. API RP 2SK. Recommended practice for design and analysis of stationkeeping systems for floating structures, 3rd Edition. 2005.
13. Pham Khac Hung et al. Estimation of the Total Reliability of Offshore Structures in Vietnam Sea Conditions Combining the Ultimate States and Fatigue Limit States. Proceedings of the OCEANS’04 MTS/IEEE/TECHNO- OCEAN/04, Kobe, Japan. 2004: p.176 - 185.
14. Palle Thoft-Christensen and Michael J.Baker. Structural reliability theory and its Applications. Springer- Verlag Berlin - New York. 1982.
15. J.V.Vietsovpetro R&D Institue. Enviromental design criteria extreme conditions for the Bach Ho-Rong fields, South-East offshore Viet Nam. Report in Vietsovpetro, Viet Nam. 2000.
16. Phạm Khắc Hùng, Phạm Hiền Hậu và nnk. Báo cáo tổng hợp kết quả KHCN đề tài nghiên cứu điều kiện kỹ thuật môi trường biển và nền móng công trình nhằm xác định luận chứng kinh tế kỹ thuật xây dựng công trình biển vùng nước sâu Việt Nam. KC.09.15/06-10. Bộ Khoa học Công nghệ. 2011.
17. Phạm Khắc Hùng, Phạm Hiền Hậu. Phương pháp luận đánh giá an toàn cho các công trình biển dựa trên các điều kiện bền và mỏi mở rộng. Hội nghị Khoa học và Công nghệ biển toàn quốc lần thứ V. Hà Nội. 10/2011; 6: trang 205 - 216.
Estimation of total reliability of FPSO’s mooring system using the probability method and its application to Vietnam’s sea conditions
Pham Hien Hau
National University of Civil Engineering
Email: hauph@nuce.edu.vn
Summary
The accident analysis of the CALM Soft Yoke FSO’s mooring lines of Vietsovpetro at the Bach Ho field [1] shows the urgent need for developing the offshore structures (including FPSO) which can be safely designed, installed and operated in the severe conditions of Vietnam’s sea. A general research on the mooring systems of floating offshore structures has been realised by the author based on consideration of several continuous problems: the second-order hydrodynamic forces, random dynamic respons- es, random fatigue damage analysis and estimation of the fatigue life of the mooring lines. In a subsequent research, the author proposed a new approach, which is closer to the real condition of the loaded mooring system, for estimat- ing the total reliability of the mooring system by the probability method. The total reliability is determined in the extreme conditions of the sea taking into account the process of cumulative fatigue damage of the mooring lines. Finally, in the applied research, the author calculated the mooring systems of FSO “VSP-01”at the Bach Ho field in Vietnam's sea. This research is based on a co-authors patent [2] and the book written by the author, published by "Presses Académiques Francophones" (PAF) in the Federal Republic of Germany [3].
Key words: Reliability, second-order hydrodynamic forces, random dynamic responses, random fatigue damage, fatigue life, mooring lines, FPSO, FSO.