Tóm tắt

Khi tính toán đánh giá trữ lượng mỏ khí ẩm với tỷ lệ condensate - khí (CGR) thấp, các thông số PVT chất lưu có ý nghĩa rất quan trọng, đặc biệt là hệ số thể tích khí (Bg). Trong quá trình khai thác từ vỉa (có nhiệt độ và áp suất cao) do việc giảm áp, khí sẽ giãn nở (thể hiện qua hệ số Bg). Nếu không có số liệu PVT từ phòng thí nghiệm thì có thể sử dụng các phương trình trạng thái (EOS) để tính toán hệ số Bg.

Bài báo phân tích và so sánh các phương pháp xác định hệ số Bg của mỏ Thiên Nga dựa trên các phương trình trạng thái như Van der Waals, Redlich-Kwong, Soave-Redlich-Kwong, Peng-Robinson, Standing-Katz. Kết quả tính toán cho thấy việc sử dụng phương trình trạng thái Peng-Robinson có sai số thấp nhất (chỉ 1,3% so với dữ liệu phân tích PVT), rất hiệu quả khi đánh giá tính chất khí, trữ lượng tại chỗ của vỉa khí ẩm.

Từ khóa: PVT, khí ẩm, hệ số thể tích khí, hệ số nén khí thiên nhiên, mỏ Thiên Nga.

1. Giới thiệu

Đánh giá trữ lượng khí tại chỗ ban đầu của vỉa khí ẩm tương đối đơn giản vì không có pha lỏng trong vỉa chứa. Tuy nhiên, yếu tố cần cân nhắc duy nhất trong việc đánh giá trữ lượng khí ban đầu tại chỗ (GIIP) là Bg. Hệ số nén khí thiên nhiên (z) được sử dụng trong tính toán Bg (như phương trình (6)). Trong trường hợp thiếu các nghiên cứu đầy đủ về tính chất PVT của chất lưu thì hệ số z sẽ được đánh giá bằng cách sử dụng các phương trình trạng thái khác nhau thông qua thành phần khí hoặc tỷ trọng khí. Các nghiên cứu đã công bố đưa ra các phương pháp tính hệ số z khác nhau dựa trên tài liệu thành phần khí hoặc tỷ trọng khí. Năm 1942, Standing và Katz [1] đã đưa ra một hàm tương quan để đánh giá hệ số z. Phương pháp này yêu cầu thành phần khí hoặc ít nhất là tỷ trọng khí để tính toán. Yarborough và Hall [2] đã phát triển một phương trình đơn giản cho tính toán trực tiếp hệ số z từ giả áp suất và giả nhiệt độ. Sutton [3], Dranchuk và Abou-Kassem [4] cũng đưa ra các phương trình tương quan để đánh giá các tính chất giả tới hạn từ tỷ trọng khí, phù hợp với biểu đồ của Standing-Katz. Kessler và Lee [5] đề xuất cách đánh giá các tính chất giả tới hạn của thành phần C7+ từ tỷ trọng khí, có thể được sử dụng trong việc tính toán hệ số z. Wichert và Aziz [6] đã phát triển một số hàm tương quan khi trong thành phần khí có CO2, N2 và H2S. Vì vậy, mô hình phương trình trạng thái như phương trình (4) có thể được xây dựng dựa trên việc sử dụng các phương trình trạng thái từ số liệu thành phần khí. Tuy nhiên, nếu các thí nghiệm PVT được làm đầy đủ thì các kết quả có thể được sử dụng để đưa ra mô hình PVT chính xác hơn để đánh giá chính xác tính chất khí và từ đó đánh giá thể tích và trữ lượng tại chỗ.

Trong bài báo này, nhóm tác giả nghiên cứu ảnh hưởng của các phương pháp khác nhau như Van der Waals [7], Redlich-Kwong [8], Soave-Redlich-Kwong [8], Peng-Robinson [9], Standing-Katz đến việc tính toán hệ số z, sau đó đánh giá ảnh hưởng của hệ số nén Z tới trữ lượng tại chỗ của khí GIIP và thu hồi. Sau đó, so sánh các kết quả tính với dữ liệu PVT từ phòng thí nghiệm để hiệu chỉnh giá trị của dữ liệu PVT ở phòng thí nghiệm trong đánh giá trữ lượng tại chỗ GIIP và thu hồi.

2. Phân loại các loại chất lưu vỉa dầu khí

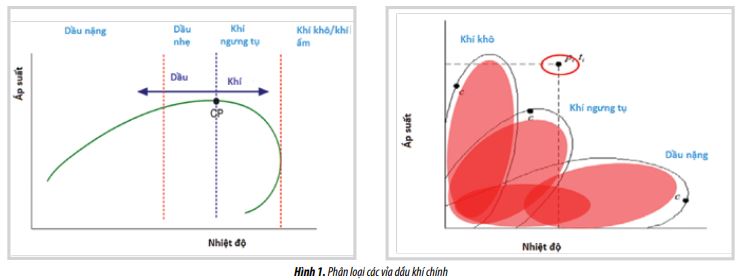
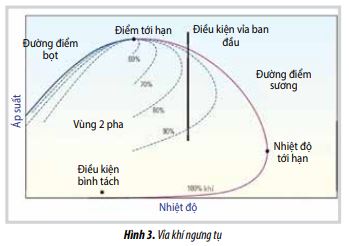
Chất lưu vỉa dầu khí chia làm 2 loại dầu và khí. Phân loại phụ của mỗi loại chính dựa trên thành phần, vị trí tương đối của điều kiện áp suất và nhiệt độ vỉa. Hình 1 thể hiện sự phân loại chính của các chất lưu sử dụng đồ thị P-T. Trong đó, các vỉa khí có thể được chia thành 3 loại gồm: vỉa khí khô, khí ẩm và khí ngưng tụ. Các vỉa khí khô và khí ẩm chỉ có một pha khí trong vỉa. Tuy nhiên, trong trường hợp khí ẩm, các giọt pha lỏng rơi ra trong hệ thống khai thác và thiết bị tách trên mặt, cũng như toàn bộ hệ thống khai thác. Hình 2 thể hiện đồ thị P-T của vỉa khí khô/ ẩm. Ngược lại, trong các vỉa khí ngưng tụ, khi áp suất giảm xuống dưới điểm sương thì chất lỏng bắt đầu xuất hiện. Phần lỏng tích tụ lại và lưu lượng khai thác bắt đầu giảm dần khi vỉa đi vào giai đoạn suy kiệt. Quá trình này được thể hiện trong Hình 3.

Tính toán trữ lượng và GIIP

Việc tính toán GIIP và trữ lượng yêu cầu các thông số đầu vào khác nhau. Đánh giá các thông số này bao gồm việc thu thập và phân tích một số lượng dữ liệu lớn như dữ liệu địa chấn, địa vật lý giếng khoan, dữ liệu phân tích mẫu/chất lưu PVT. Dưới đây là phương trình tính toán GIIP từ tính chất vỉa và chất lưu thông thường.

Khí vỉa là khí thực, phương trình trạng thái đơn giản nhất có thể được miêu tả bằng phương trình (4)[10] như sau:

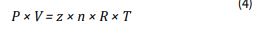
Áp dụng phương trình (4) tại điều kiện vỉa và điều kiện tiêu chuẩn. Phương trình (3) trở thành:

Phương trình (1) cho thấy hệ số thể tích khí là thông số quan trọng trong đánh giá GIIP và trữ lượng. Ví dụ, hệ số này chỉ sai số 10% sẽ cho kết quả tính toán GIIP và trữ lượng sai số 10%. Hình 4 chỉ ra rằng đối với khí thiên nhiên, z = 1 ở điều kiện tiêu chuẩn (14,7psia và 60oF) và giá trị này có thể thay đổi từ 0,25-1,7 như hàm giả áp suất và giả nhiệt độ, tức là áp suất và nhiệt độ thực tế và tới hạn. Áp suất và nhiệt độ tới hạn của hỗn hợp khí (khí tự nhiên là hỗn hợp của nhiều hydrocarbon khác nhau, CO2, N2, H2S…), phụ thuộc vào thành phần của hỗn hợp. Vì vậy, tính chính xác về tính chất chất lưu vỉa (trong trường hợp này là khí) rất cần thiết để dự báo GIIP, trữ lượng và khai thác. Đây là mục tiêu chính của nghiên cứu PVT trong phòng thí nghiệm. Điều này được gọi là đặc tính PVT.

4. Đặc tính PVT của vỉa khí ẩm

Tính chính xác của tính chất PVT chất lưu vỉa chứa là cần thiết để đánh giá chính xác GIIP, trữ lượng và dự báo khai thác. Một nghiên cứu đặc tính PVT gồm phân tích thành phần của mẫu trên mặt và/hoặc mẫu ở đáy giếng và mẫu ở các pha của bình tách kết hợp với các phân tích khác nhau trong phòng thí nghiệm (CCE, CVD, tách nhiều bậc…). Tỷ lệ pha và các điểm chuyển tiếp pha (nếu có) cũng được đo sẽ kết hợp trong các phân tích trong phòng thí nghiệm. Từ đó lựa chọn phương trình tính toán tối ưu nhất. Phương trình này sẽ xác định thêm một số thành phần mà trong phòng thí nghiệm không thể xác định được và các tham số
nhiệt động lực học sau đó cộng gộp chúng lại và hiệu chỉnh dựa trên kết quả thực tế từ phòng thí nghiệm và trong quá trình khai thác.

5. Phương trình trạng thái của khí hydrocarbon

Phương trình trạng thái là các mô hình toán học có thể mô tả và dự báo áp suất, thể tích, mối quan hệ với nhiệt độ cho loại chất lưu nghiên cứu do không thể thực hiện được các thí nghiệm cho từng điều kiện áp suất nhiệt độ của chất lưu trong suốt đời mỏ. Phương trình (4): P × V = z × n× R × T được gọi là phương trình trạng thái nén. Khó khăn chính là việc xác định chính xác hệ số z đối với mỏ khí thiên nhiên. Nhiều phương trình trạng thái đã được đưa ra với mục tiêu đánh giá độ lệch về trạng thái PVT từ khí lý tưởng, tương đương với hệ số z.

Một số các phương trình dùng để tính toán như sau:

Peng-Robinson cũng tiếp cận cách tính hệ số α của Soave. α là thông số không thứ nguyên được xác định theo công thức sau:

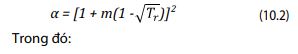
Giải phương trình bậc 3 trên lấy giá trị lớn nhất là hệ số nén z của khí và giá trị thấp nhất là thành phần lỏng.

Trên cơ sở thử vỉa, đo địa vật lý giếng khoan và kết quả mẫu chỉ ra mỏ Thiên Nga là mỏ khí ẩm với CGR thấp chỉ khoảng 9,8bbls/ mmscf. Các mẫu PVT được lấy từ đáy giếng và bình tách và được phân tích trong phòng thí nghiệm. Sử dụng các phương trình tính toán trên cho thấy sai số trong tính toán hệ số thể tích của khí (Bảng 4).

Bảng 1 và 2 thể hiện thành phần và thông số điều kiện vỉa của mỏ Thiên Nga. Trước khi tính toán hệ số thể tích Bg, kết quả PVT sẽ được kiểm tra độ tin cậy dựa trên hệ số cân bằng pha k (Hình 5).

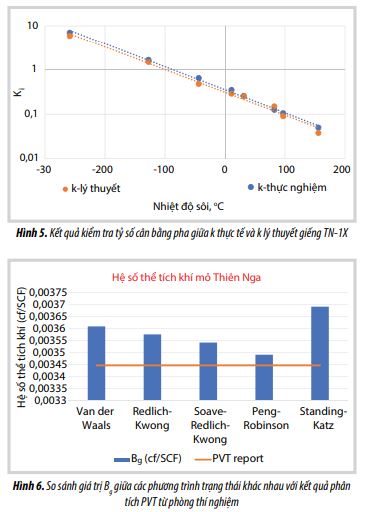
Kiểm tra kết quả phân tích PVT dựa trên tỷ số cân bằng pha k.

Bảng 3 và Hình 5 cho thấy kết quả hệ số k phân tích từ thực nghiệm sát với hệ số k lý thuyết nên kết quả phân tích PVT là tốt và đủ độ tin cậy để sử dụng cho tính toán.

Kết quả tính toán hệ số thể tích đối với mỏ Thiên Nga theo các phương trình trạng thái khác nhau được thể hiện trong Bảng 4.
Từ Bảng 4 và Hình 6 cho thấy kết quả tính toán giá trị Bg bằng phương trình trạng thái của Peng-Robinson (0,003491) cho kết quả tương đương kết quả phân tích PVT từ phòng thí nghiệm (0,003447), sai số chỉ khoảng 1,3%. Việc sử dụng phương trình trạng thái Soave-Relich- Kwong có sai số 2,7% so với kết quả phân tích PVT. Các phương trình trạng thái khác cho giá trị Bg cao hơn từ 3,6- 6,6%. Có thể thấy việc lựa chọn phương pháp tính Bg sẽ ảnh hưởng lớn tới kết quả đánh giá trữ lượng, GIIP của mỏ khí ẩm.

6. Kết luận

Việc lựa chọn phương trình tối ưu để tính toán hệ số thể tích của khí rất quan trọng vì ảnh hưởng rất lớn đến kết quả tính toán trữ lượng trong trường hợp không có số liệu đo PVT.

Phương trình trạng thái Peng-Robinson cho thấy hiệu quả cao nhất khi có sai số thấp (1,3%) so với số liệu đo PVT. Do đó trong trường hợp không có đủ số liệu đo PVT có thể sử dụng phương trình trạng thái Peng-Robinson để tính toán hệ số thể tích của khí ẩm.

Tài liệu tham khảo

1. Marshall B.Standing, Donald L.Katz. Density of natural gases. Society of Petroleum Engineers. 1942; 146(1).

2. Lyman Yarborrough, Kenneth R.Hall. How to solve equation of state for Z-factor. Oil and Gas Journal. 1974; 72(7): p. 86 - 88.

3. R.P.Sutton. Compressibility factors for high- molecualr-weight reservoir gases. SPE Annual Technical Conference and Exhibition, Las Vegas, Nevada. 22 - 26 September, 1985.

4. P.M.Dranchuk, H.Abou-Kassem. Calculation of Z-factors for natural gas using equation of state. Journal of Canadian Petroleum Technology. 1975; 14(3).

5. Michael G.Kessler, Byung Ik Lee. Improved predictionofenthalpyoffractions. Hydrocarbon Processing. 1976; 55(3): p. 153 - 158.

6. E.Wichert, K.Aziz. Calculate Z’s for sour gases. Hydrocarbon Processing. 1972; 51(5): p. 119 - 122.

7. Van der Waals, J.D. Over de continuieit van den Gas-en Vloeistoftoestand. Leiden: Boekdrukkerij Van A.W.Sijthoff. 1873.

8. Otto Redlich, J.N.S.Kwong. On the thermodynamics of solutions. V.An equation of state. Fugacities of gaseous solution. Chemical Reviews. 1949; 44(1): p. 233 - 244.

9. Ding-Yu.Peng, Donald B.Robinson. A New two-constant equation of state. Industrial & Engineering Chemistry Fundamentals. 1965; 15(1): p. 59 - 64.

10. J.Q.Cope, W.K.Lewis, H.C.Wesber. Generalized thermodynamic properties of higher hydrocarbon vapors. Indutrial Engineering Chemistry. 1931; 23(8): p. 887 - 892.

11. Ding-Yu Peng, Donald B.Robinson. A new two- constant equation of state. Industrial & Engineering Chemistry Fundamentals. 1976; 15(1): p. 59 - 64.

12. Hamad Al Marri, Akim, Saudi Aramco. PVT characterization of a wet gas reservoir and its impact on reserves estimate. SPE Saudi Arabia Section Annual Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia. 21 - 23 April, 2015.

13. Tarek Ahmed. Equations of state and PVT analysis - Application for improved reservoir modeling. 2016.

14. Vietsovpetro. Báo cáo phân tích PVT mỏ Thiên Nga. 2016.

EFFECT OF THE SELECTION OF STATE EQUATIONS ON RESERVE ESTIMATE OF WET GAS RESERVOIR

Nguyen Van Do, Tran Van Tien - Vietnam Petroleum Institute 
Email: donv@vpi.pvn.vn

Summary

PVT parameters, especially formation volume factor (Bg), are very important in Gas Initial in Place (GIIP) estimate of wet gas reser- voir which has very low condensate to gas ratio (CGR). During the process of gas production from reservoir (with high temperature, high pressure) to surface, gas will expand due to decreasing pressure, which is indicated by the formation volume factor (Bg). In the absence of laboratory PVT data, equations of states (EOS) can be used to estimate the Bgfactor.

The paper analyses and compares methods of determining Bgfor Thien Nga field based on equations of states such as Van der Waals, Redlich-Kwong, Soave-Redlich-Kwong, Peng-Robinson, and Standing-Katz. The results show the difference of Bg between PVT data and determination of Peng-Robinson EOS is the lowest, only 1,3%. Wherefore, Peng-Robinsonequation of state is themostreliablemethodin evaluation of gas properties and GIIP of the wet gas reservoir.

Key words: PVT, wet gas, formation volume factor, natural gas compression factor, Thien Nga field.